Modern neural networks have achieved spectacular efficiency throughout a wide range of purposes, equivalent to language, mathematical reasoning, and imaginative and prescient. However, these networks typically use giant architectures that require a number of computational sources. This could make it impractical to serve such fashions to customers, particularly in resource-constrained environments like wearables and smartphones. A extensively used strategy to mitigate the inference prices of pre-trained networks is to prune them by eradicating a few of their weights, in a approach that doesn’t considerably have an effect on utility. In normal neural networks, every weight defines a connection between two neurons. So after weights are pruned, the enter will propagate by a smaller set of connections and thus requires much less computational sources.
 |
| Original community vs. a pruned community. |
Pruning strategies might be utilized at totally different levels of the community’s coaching course of: publish, throughout, or earlier than coaching (i.e., instantly after weight initialization). In this publish, we deal with the post-training setting: given a pre-trained community, how can we decide which weights needs to be pruned? One in style methodology is magnitude pruning, which removes weights with the smallest magnitude. While environment friendly, this methodology doesn’t immediately contemplate the impact of eradicating weights on the community’s efficiency. Another in style paradigm is optimization-based pruning, which removes weights based mostly on how a lot their removing impacts the loss perform. Although conceptually interesting, most present optimization-based approaches appear to face a severe tradeoff between efficiency and computational necessities. Methods that make crude approximations (e.g., assuming a diagonal Hessian matrix) can scale nicely, however have comparatively low efficiency. On the opposite hand, whereas strategies that make fewer approximations are likely to carry out higher, they look like a lot much less scalable.
In “Fast as CHITA: Neural Network Pruning with Combinatorial Optimization”, introduced at ICML 2023, we describe how we developed an optimization-based strategy for pruning pre-trained neural networks at scale. CHITA (which stands for “Combinatorial Hessian-free Iterative Thresholding Algorithm”) outperforms present pruning strategies by way of scalability and efficiency tradeoffs, and it does so by leveraging advances from a number of fields, together with high-dimensional statistics, combinatorial optimization, and neural community pruning. For instance, CHITA might be 20x to 1000x sooner than state-of-the-art strategies for pruning ResNet and improves accuracy by over 10% in lots of settings.
Overview of contributions
CHITA has two notable technical enhancements over in style strategies:
- Efficient use of second-order data: Pruning strategies that use second-order data (i.e., regarding second derivatives) obtain the cutting-edge in lots of settings. In the literature, this data is often utilized by computing the Hessian matrix or its inverse, an operation that could be very troublesome to scale as a result of the Hessian dimension is quadratic with respect to the variety of weights. Through cautious reformulation, CHITA makes use of second-order data with out having to compute or retailer the Hessian matrix explicitly, thus permitting for extra scalability.
- Combinatorial optimization: Popular optimization-based strategies use a easy optimization method that prunes weights in isolation, i.e., when deciding to prune a sure weight they don’t take into consideration whether or not different weights have been pruned. This might result in pruning essential weights as a result of weights deemed unimportant in isolation might change into essential when different weights are pruned. CHITA avoids this concern through the use of a extra superior, combinatorial optimization algorithm that takes into consideration how pruning one weight impacts others.
In the sections under, we focus on CHITA’s pruning formulation and algorithms.
A computation-friendly pruning formulation
There are many attainable pruning candidates, that are obtained by retaining solely a subset of the weights from the unique community. Let okay be a user-specified parameter that denotes the variety of weights to retain. Pruning might be naturally formulated as a best-subset choice (BSS) drawback: amongst all attainable pruning candidates (i.e., subsets of weights) with solely okay weights retained, the candidate that has the smallest loss is chosen.
 |
| Pruning as a BSS drawback: amongst all attainable pruning candidates with the identical whole variety of weights, the most effective candidate is outlined because the one with the least loss. This illustration exhibits 4 candidates, however this quantity is mostly a lot bigger. |
Solving the pruning BSS drawback on the unique loss perform is mostly computationally intractable. Thus, just like earlier work, equivalent to OBD and OBS, we approximate the loss with a quadratic perform through the use of a second-order Taylor sequence, the place the Hessian is estimated with the empirical Fisher data matrix. While gradients might be usually computed effectively, computing and storing the Hessian matrix is prohibitively costly as a result of its sheer dimension. In the literature, it is not uncommon to cope with this problem by making restrictive assumptions on the Hessian (e.g., diagonal matrix) and in addition on the algorithm (e.g., pruning weights in isolation).
CHITA makes use of an environment friendly reformulation of the pruning drawback (BSS utilizing the quadratic loss) that avoids explicitly computing the Hessian matrix, whereas nonetheless utilizing all the knowledge from this matrix. This is made attainable by exploiting the low-rank construction of the empirical Fisher data matrix. This reformulation might be seen as a sparse linear regression drawback, the place every regression coefficient corresponds to a sure weight within the neural community. After acquiring an answer to this regression drawback, coefficients set to zero will correspond to weights that needs to be pruned. Our regression information matrix is (n x p), the place n is the batch (sub-sample) dimension and p is the variety of weights within the authentic community. Typically n << p, so storing and working with this information matrix is far more scalable than frequent pruning approaches that function with the (p x p) Hessian.
 |
| CHITA reformulates the quadratic loss approximation, which requires an costly Hessian matrix, as a linear regression (LR) drawback. The LR’s information matrix is linear in p, which makes the reformulation extra scalable than the unique quadratic approximation. |
Scalable optimization algorithms
CHITA reduces pruning to a linear regression drawback beneath the next sparsity constraint: at most okay regression coefficients might be nonzero. To receive an answer to this drawback, we contemplate a modification of the well-known iterative exhausting thresholding (IHT) algorithm. IHT performs gradient descent the place after every replace the next post-processing step is carried out: all regression coefficients outdoors the Top-okay (i.e., the okay coefficients with the biggest magnitude) are set to zero. IHT usually delivers resolution to the issue, and it does so iteratively exploring totally different pruning candidates and collectively optimizing over the weights.
Due to the dimensions of the issue, normal IHT with fixed studying charge can undergo from very sluggish convergence. For sooner convergence, we developed a brand new line-search methodology that exploits the issue construction to discover a appropriate studying charge, i.e., one which results in a sufficiently giant lower within the loss. We additionally employed a number of computational schemes to enhance CHITA’s effectivity and the standard of the second-order approximation, resulting in an improved model that we name CHITA++.
Experiments
We examine CHITA’s run time and accuracy with a number of state-of-the-art pruning strategies utilizing totally different architectures, together with ResNet and MobileNet.
Run time: CHITA is far more scalable than comparable strategies that carry out joint optimization (versus pruning weights in isolation). For instance, CHITA’s speed-up can attain over 1000x when pruning ResNet.
Post-pruning accuracy: Below, we examine the efficiency of CHITA and CHITA++ with magnitude pruning (MP), Woodfisher (WF), and Combinatorial Brain Surgeon (CBS), for pruning 70% of the mannequin weights. Overall, we see good enhancements from CHITA and CHITA++.
 |
| Post-pruning accuracy of assorted strategies on ResNet20. Results are reported for pruning 70% of the mannequin weights. |
 |
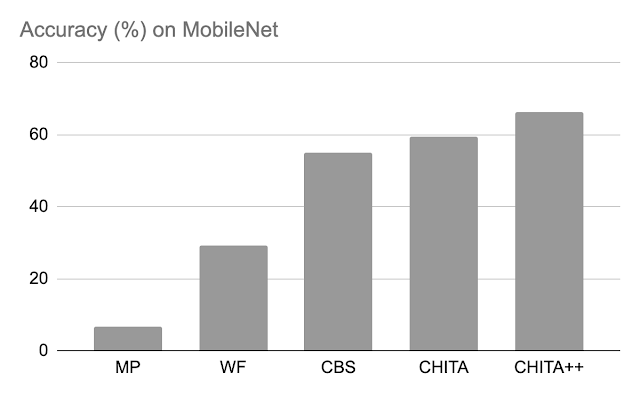| Post-pruning accuracy of assorted strategies on MobileNet. Results are reported for pruning 70% of the mannequin weights. |
Next, we report outcomes for pruning a bigger community: ResNet50 (on this community, among the strategies listed within the ResNet20 determine couldn’t scale). Here we examine with magnitude pruning and M-FAC. The determine under exhibits that CHITA achieves higher take a look at accuracy for a variety of sparsity ranges.
 |
| Test accuracy of pruned networks, obtained utilizing totally different strategies. |
Conclusion, limitations, and future work
We introduced CHITA, an optimization-based strategy for pruning pre-trained neural networks. CHITA gives scalability and aggressive efficiency by effectively utilizing second-order data and drawing on concepts from combinatorial optimization and high-dimensional statistics.
CHITA is designed for unstructured pruning during which any weight might be eliminated. In principle, unstructured pruning can considerably scale back computational necessities. However, realizing these reductions in apply requires particular software program (and probably {hardware}) that help sparse computations. In distinction, structured pruning, which removes complete constructions like neurons, might provide enhancements which might be simpler to realize on general-purpose software program and {hardware}. It could be attention-grabbing to increase CHITA to structured pruning.
Acknowledgements
This work is a part of a analysis collaboration between Google and MIT. Thanks to Rahul Mazumder, Natalia Ponomareva, Wenyu Chen, Xiang Meng, Zhe Zhao, and Sergei Vassilvitskii for his or her assist in making ready this publish and the paper. Also because of John Guilyard for creating the graphics on this publish.