Dynamic linear fashions with tfprobability

By
Ztec 100
-
0
107
Dynamic linear fashions with tfprobability


Welcome to the world of state area fashions. In this world, there’s a latent course of, hidden from our eyes; and there are observations we make in regards to the issues it produces. The course of evolves because of some hidden logic (transition mannequin); and the way in which it produces the observations follows some hidden logic (commentary mannequin). There is noise in course of evolution, and there may be noise in commentary. If the transition and commentary fashions each are linear, and the method in addition to commentary noise are Gaussian, we now have a linear-Gaussian state area mannequin (SSM). The process is to deduce the latent state from the observations. The most well-known method is the Kálmán filter.

In sensible purposes, two traits of linear-Gaussian SSMs are particularly engaging.

For one, they allow us to estimate dynamically altering parameters. In regression, the parameters could be seen as a hidden state; we could thus have a slope and an intercept that modify over time. When parameters can fluctuate, we communicate of dynamic linear fashions (DLMs). This is the time period we’ll use all through this put up when referring to this class of fashions.

Second, linear-Gaussian SSMs are helpful in time-series forecasting as a result of Gaussian processes could be added. A time sequence can thus be framed as, e.g. the sum of a linear pattern and a course of that varies seasonally.

Using tfprobability, the R wrapper to TensorFlow Probability, we illustrate each features right here. Our first instance might be on dynamic linear regression. In an in depth walkthrough, we present on the best way to match such a mannequin, the best way to acquire filtered, in addition to smoothed, estimates of the coefficients, and the best way to acquire forecasts.
Our second instance then illustrates course of additivity. This instance will construct on the primary, and might also function a fast recap of the general process.

Let’s soar in.

Dynamic linear regression instance: Capital Asset Pricing Model (CAPM)

Our code builds on the not too long ago launched variations of TensorFlow and TensorFlow Probability: 1.14 and 0.7, respectively.

Note how there’s one factor we used to do recently that we’re not doing right here: We’re not enabling keen execution. We say why in a minute.

Our instance is taken from Petris et al.(2009)(Petris, Petrone, and Campagnoli 2009), chapter 3.2.7.
Besides introducing the dlm package deal, this guide supplies a pleasant introduction to the concepts behind DLMs normally.

To illustrate dynamic linear regression, the authors characteristic a dataset, initially from Berndt(1991)(Berndt 1991) that has month-to-month returns, collected from January 1978 to December 1987, for 4 totally different shares, the 30-day Treasury Bill – standing in for a risk-free asset –, and the value-weighted common returns for all shares listed on the New York and American Stock Exchanges, representing the general market returns.

Let’s have a look.

# As the information doesn't appear to be accessible on the tackle given in Petris et al. any extra,
# we put it on the weblog for obtain
# obtain from: 
# https://github.com/rstudio/tensorflow-blog/blob/master/docs/posts/2019-06-25-dynamic_linear_models_tfprobability/data/capm.txt"
df <- read_table(
  "capm.txt",
  col_types = checklist(X1 = col_date(format = "%Y.%m"))) %>%
  rename(month = X1)
df %>% glimpse()
Observations: 120
Variables: 7
$ month  <date> 1978-01-01, 1978-02-01, 1978-03-01, 1978-04-01, 1978-05-01, 19…
$ MOBIL  <dbl> -0.046, -0.017, 0.049, 0.077, -0.011, -0.043, 0.028, 0.056, 0.0…
$ IBM    <dbl> -0.029, -0.043, -0.063, 0.130, -0.018, -0.004, 0.092, 0.049, -0…
$ WEYER  <dbl> -0.116, -0.135, 0.084, 0.144, -0.031, 0.005, 0.164, 0.039, -0.0…
$ CITCRP <dbl> -0.115, -0.019, 0.059, 0.127, 0.005, 0.007, 0.032, 0.088, 0.011…
$ MARKET <dbl> -0.045, 0.010, 0.050, 0.063, 0.067, 0.007, 0.071, 0.079, 0.002,…
$ RKFREE <dbl> 0.00487, 0.00494, 0.00526, 0.00491, 0.00513, 0.00527, 0.00528, …
df %>% collect(key = "image", worth = "return", -month) %>%
  ggplot(aes(x = month, y = return, coloration = image)) +
  geom_line() +
  facet_grid(rows = vars(image), scales = "free")

Monthly returns for selected stocks; data from Berndt (1991).

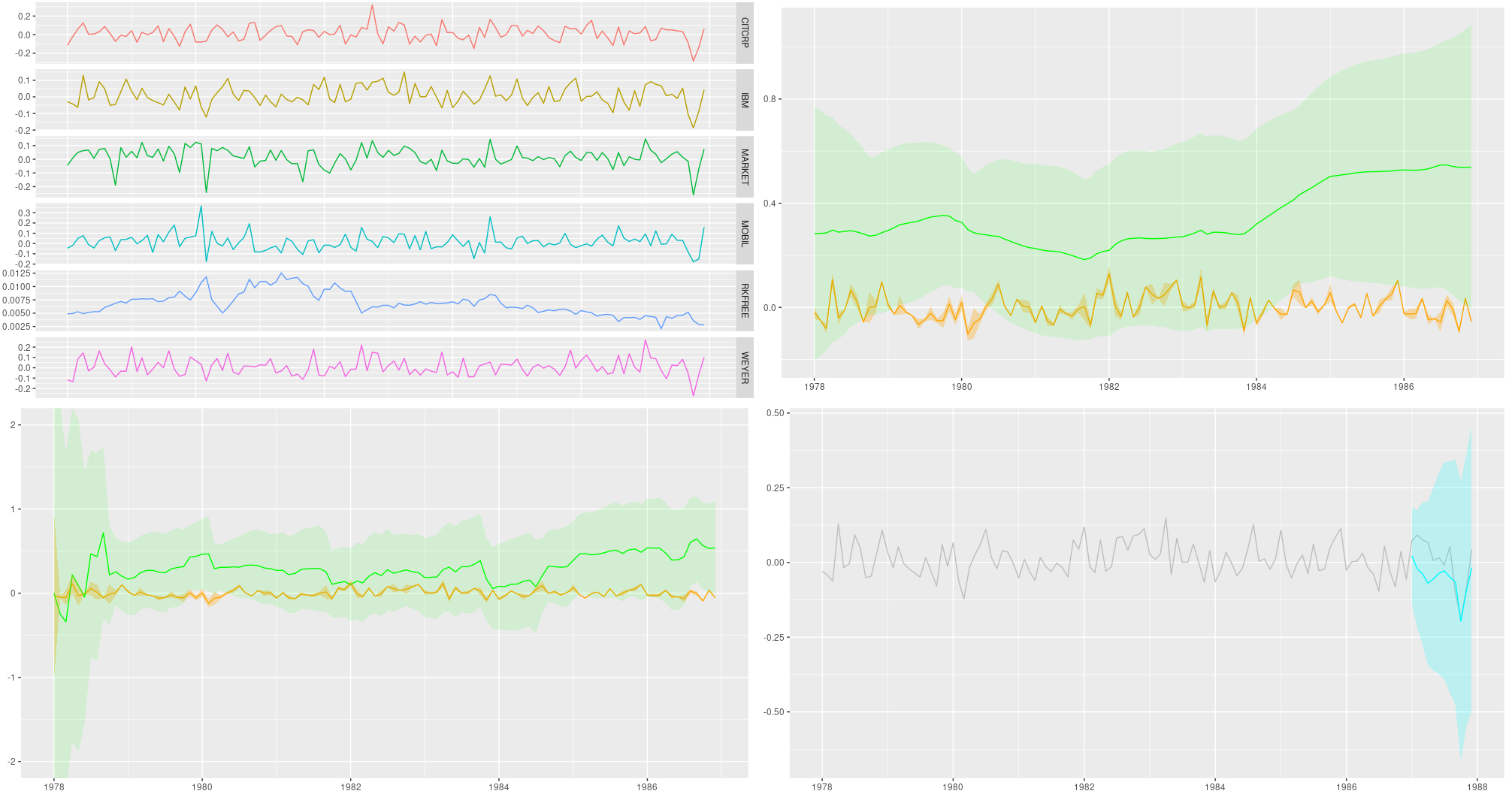
Figure 1: Monthly returns for chosen shares; knowledge from Berndt (1991).

The Capital Asset Pricing Model then assumes a linear relationship between the surplus returns of an asset beneath research and the surplus returns of the market. For each, extra returns are obtained by subtracting the returns of the chosen risk-free asset; then, the scaling coefficient between them reveals the asset to both be an “aggressive” funding (slope > 1: adjustments available in the market are amplified), or a conservative one (slope < 1: adjustments are damped).

Assuming this relationship doesn’t change over time, we will simply use lm as an instance this. Following Petris et al. in zooming in on IBM because the asset beneath research, we now have

# extra returns of the asset beneath research
ibm <- df$IBM - df$RKFREE
# market extra returns
x <- df$MARKET - df$RKFREE

match <- lm(ibm ~ x)
abstract(match)
Call:
lm(method = ibm ~ x)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.11850 -0.03327 -0.00263  0.03332  0.15042 

Coefficients:
              Estimate Std. Error t worth Pr(>|t|)    
(Intercept) -0.0004896  0.0046400  -0.106    0.916    
x            0.4568208  0.0675477   6.763 5.49e-10 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual commonplace error: 0.05055 on 118 levels of freedom
Multiple R-squared:  0.2793,    Adjusted R-squared:  0.2732 
F-statistic: 45.74 on 1 and 118 DF,  p-value: 5.489e-10

So IBM is discovered to be a conservative funding, the slope being ~ 0.5. But is that this relationship steady over time?

Let’s flip to tfprobability to research.

We wish to use this instance to exhibit two important purposes of DLMs: acquiring smoothing and/or filtering estimates of the coefficients, in addition to forecasting future values. So in contrast to Petris et al., we divide the dataset right into a coaching and a testing half:.

# zoom in on ibm
ts <- ibm %>% matrix()
# forecast 12 months
n_forecast_steps <- 12
ts_train <- ts[1:(length(ts) - n_forecast_steps), 1, drop = FALSE]

# be sure that we work with float32 right here
ts_train <- tf$forged(ts_train, tf$float32)
ts <- tf$forged(ts, tf$float32)

We now assemble the mannequin. sts_dynamic_linear_regression() does what we would like:

# outline the mannequin on the whole sequence
linreg <- ts %>%
  sts_dynamic_linear_regression(
    design_matrix = cbind(rep(1, size(x)), x) %>% tf$forged(tf$float32)
  )

We move it the column of extra market returns, plus a column of ones, following Petris et al.. Alternatively, we might middle the one predictor – this may work simply as effectively.

How are we going to coach this mannequin? Method-wise, we now have a alternative between variational inference (VI) and Hamiltonian Monte Carlo (HMC). We will see each. The second query is: Are we going to make use of graph mode or keen mode? As of at this time, for each VI and HMC, it’s most secure – and quickest – to run in graph mode, so that is the one method we present. In just a few weeks, or months, we should always be capable to prune loads of sess$run()s from the code!

Normally in posts, when presenting code we optimize for simple experimentation (which means: line-by-line executability), not modularity. This time although, with an necessary variety of analysis statements concerned, it’s best to pack not simply the becoming, however the smoothing and forecasting as effectively right into a operate (which you possibly can nonetheless step by if you happen to needed). For VI, we’ll have a match _with_vi operate that does all of it. So once we now begin explaining what it does, don’t kind within the code simply but – it’ll all reappear properly packed into that operate, so that you can copy and execute as a complete.

Fitting a time sequence with variational inference

Fitting with VI just about seems to be like coaching historically used to look in graph-mode TensorFlow. You outline a loss – right here it’s completed utilizing sts_build_factored_variational_loss() –, an optimizer, and an operation for the optimizer to scale back that loss:

optimizer <- tf$compat$v1$prepare$AdamOptimizer(0.1)

# solely prepare on the coaching set!    
loss_and_dists <- ts_train %>% sts_build_factored_variational_loss(mannequin = mannequin)
variational_loss <- loss_and_dists[[1]]

train_op <- optimizer$decrease(variational_loss)

Note how the loss is outlined on the coaching set solely, not the whole sequence.

Now to truly prepare the mannequin, we create a session and run that operation:

 with (tf$Session() %as% sess,  {
      
      sess$run(tf$compat$v1$global_variables_initializer())
   
      for (step in 1:n_iterations) {
        res <- sess$run(train_op)
        loss <- sess$run(variational_loss)
        if (step %% 10 == 0)
          cat("Loss: ", as.numeric(loss), "n")
      }
 })

Given we now have that session, let’s make use of it and compute all of the estimates we want.
Again, – the next snippets will find yourself within the fit_with_vi operate, so don’t run them in isolation simply but.

Obtaining forecasts

The very first thing we would like for the mannequin to offer us are forecasts. In order to create them, it wants samples from the posterior. Luckily we have already got the posterior distributions, returned from sts_build_factored_variational_loss, so let’s pattern from them and move them to sts_forecast:

variational_distributions <- loss_and_dists[[2]]
posterior_samples <-
  Map(
    operate(d) d %>% tfd_sample(n_param_samples),
    variational_distributions %>% reticulate::py_to_r() %>% unname()
  )
forecast_dists <- ts_train %>% sts_forecast(mannequin, posterior_samples, n_forecast_steps)

sts_forecast() returns distributions, so we name tfd_mean() to get the posterior predictions and tfd_stddev() for the corresponding commonplace deviations:

fc_means <- forecast_dists %>% tfd_mean()
fc_sds <- forecast_dists %>% tfd_stddev()

By the way in which – as we now have the total posterior distributions, we’re under no circumstances restricted to abstract statistics! We might simply use tfd_sample() to acquire particular person forecasts.

Smoothing and filtering (Kálmán filter)

Now, the second (and final, for this instance) factor we’ll need are the smoothed and filtered regression coefficients. The well-known Kálmán Filter is a Bayesian-in-spirit methodology the place at every time step, predictions are corrected by how a lot they differ from an incoming commentary. Filtering estimates are based mostly on observations we’ve seen to date; smoothing estimates are computed “in hindsight,” making use of the whole time sequence.

We first create a state area mannequin from our time sequence definition:

# solely do that on the coaching set
# returns an occasion of tfd_linear_gaussian_state_space_model()
ssm <- mannequin$make_state_space_model(size(ts_train), param_vals = posterior_samples)

tfd_linear_gaussian_state_space_model(), technically a distribution, supplies the Kálmán filter functionalities of smoothing and filtering.

To acquire the smoothed estimates:

c(smoothed_means, smoothed_covs) %<-% ssm$posterior_marginals(ts_train)

And the filtered ones:

c(., filtered_means, filtered_covs, ., ., ., .) %<-% ssm$forward_filter(ts_train)

Finally, we have to consider all these.

c(posterior_samples, fc_means, fc_sds, smoothed_means, smoothed_covs, filtered_means, filtered_covs) %<-%
  sess$run(checklist(posterior_samples, fc_means, fc_sds, smoothed_means, smoothed_covs, filtered_means, filtered_covs))

Putting all of it collectively (the VI version)

So right here’s the whole operate, fit_with_vi, prepared for us to name.

fit_with_vi <-
  operate(ts,
           ts_train,
           mannequin,
           n_iterations,
           n_param_samples,
           n_forecast_steps,
           n_forecast_samples) {
    
    optimizer <- tf$compat$v1$prepare$AdamOptimizer(0.1)
    
    loss_and_dists <-
      ts_train %>% sts_build_factored_variational_loss(mannequin = mannequin)
    variational_loss <- loss_and_dists[[1]]
    train_op <- optimizer$decrease(variational_loss)
    
    with (tf$Session() %as% sess,  {
      
      sess$run(tf$compat$v1$global_variables_initializer())
      for (step in 1:n_iterations) {
        sess$run(train_op)
        loss <- sess$run(variational_loss)
        if (step %% 1 == 0)
          cat("Loss: ", as.numeric(loss), "n")
      }
      variational_distributions <- loss_and_dists[[2]]
      posterior_samples <-
        Map(
          operate(d)
            d %>% tfd_sample(n_param_samples),
          variational_distributions %>% reticulate::py_to_r() %>% unname()
        )
      forecast_dists <-
        ts_train %>% sts_forecast(mannequin, posterior_samples, n_forecast_steps)
      fc_means <- forecast_dists %>% tfd_mean()
      fc_sds <- forecast_dists %>% tfd_stddev()
      
      ssm <- mannequin$make_state_space_model(size(ts_train), param_vals = posterior_samples)
      c(smoothed_means, smoothed_covs) %<-% ssm$posterior_marginals(ts_train)
      c(., filtered_means, filtered_covs, ., ., ., .) %<-% ssm$forward_filter(ts_train)
   
      c(posterior_samples, fc_means, fc_sds, smoothed_means, smoothed_covs, filtered_means, filtered_covs) %<-%
        sess$run(checklist(posterior_samples, fc_means, fc_sds, smoothed_means, smoothed_covs, filtered_means, filtered_covs))
      
    })
    
    checklist(
      variational_distributions,
      posterior_samples,
      fc_means[, 1],
      fc_sds[, 1],
      smoothed_means,
      smoothed_covs,
      filtered_means,
      filtered_covs
    )
  }

And that is how we name it.

# variety of VI steps
n_iterations <- 300
# pattern measurement for posterior samples
n_param_samples <- 50
# pattern measurement to attract from the forecast distribution
n_forecast_samples <- 50

# this is the mannequin once more
mannequin <- ts %>%
  sts_dynamic_linear_regression(design_matrix = cbind(rep(1, size(x)), x) %>% tf$forged(tf$float32))

# name fit_vi outlined above
c(
  param_distributions,
  param_samples,
  fc_means,
  fc_sds,
  smoothed_means,
  smoothed_covs,
  filtered_means,
  filtered_covs
) %<-% fit_vi(
  ts,
  ts_train,
  mannequin,
  n_iterations,
  n_param_samples,
  n_forecast_steps,
  n_forecast_samples
)

Curious in regards to the outcomes? We’ll see them in a second, however earlier than let’s simply rapidly look on the different coaching methodology: HMC.

Putting all of it collectively (the HMC version)

tfprobability supplies sts_fit_with_hmc to suit a DLM utilizing Hamiltonian Monte Carlo. Recent posts (e.g., Hierarchical partial pooling, continued: Varying slopes fashions with TensorFlow Probability) confirmed the best way to arrange HMC to suit hierarchical fashions; right here a single operate does all of it.

Here is fit_with_hmc, wrapping sts_fit_with_hmc in addition to the (unchanged) methods for acquiring forecasts and smoothed/filtered parameters:

num_results <- 200
num_warmup_steps <- 100

fit_hmc <- operate(ts,
                    ts_train,
                    mannequin,
                    num_results,
                    num_warmup_steps,
                    n_forecast,
                    n_forecast_samples) {
  
  states_and_results <-
    ts_train %>% sts_fit_with_hmc(
      mannequin,
      num_results = num_results,
      num_warmup_steps = num_warmup_steps,
      num_variational_steps = num_results + num_warmup_steps
    )
  
  posterior_samples <- states_and_results[[1]]
  forecast_dists <-
    ts_train %>% sts_forecast(mannequin, posterior_samples, n_forecast_steps)
  fc_means <- forecast_dists %>% tfd_mean()
  fc_sds <- forecast_dists %>% tfd_stddev()
  
  ssm <-
    mannequin$make_state_space_model(size(ts_train), param_vals = posterior_samples)
  c(smoothed_means, smoothed_covs) %<-% ssm$posterior_marginals(ts_train)
  c(., filtered_means, filtered_covs, ., ., ., .) %<-% ssm$forward_filter(ts_train)
  
  with (tf$Session() %as% sess,  {
    sess$run(tf$compat$v1$global_variables_initializer())
    c(
      posterior_samples,
      fc_means,
      fc_sds,
      smoothed_means,
      smoothed_covs,
      filtered_means,
      filtered_covs
    ) %<-%
      sess$run(
        checklist(
          posterior_samples,
          fc_means,
          fc_sds,
          smoothed_means,
          smoothed_covs,
          filtered_means,
          filtered_covs
        )
      )
  })
  
  checklist(
    posterior_samples,
    fc_means[, 1],
    fc_sds[, 1],
    smoothed_means,
    smoothed_covs,
    filtered_means,
    filtered_covs
  )
}

c(
  param_samples,
  fc_means,
  fc_sds,
  smoothed_means,
  smoothed_covs,
  filtered_means,
  filtered_covs
) %<-% fit_hmc(ts,
               ts_train,
               mannequin,
               num_results,
               num_warmup_steps,
               n_forecast,
               n_forecast_samples)

Now lastly, let’s check out the forecasts and filtering resp. smoothing estimates.

Forecasts

Putting all we’d like into one dataframe, we now have

smoothed_means_intercept <- smoothed_means[, , 1] %>% colMeans()
smoothed_means_slope <- smoothed_means[, , 2] %>% colMeans()

smoothed_sds_intercept <- smoothed_covs[, , 1, 1] %>% colMeans() %>% sqrt()
smoothed_sds_slope <- smoothed_covs[, , 2, 2] %>% colMeans() %>% sqrt()

filtered_means_intercept <- filtered_means[, , 1] %>% colMeans()
filtered_means_slope <- filtered_means[, , 2] %>% colMeans()

filtered_sds_intercept <- filtered_covs[, , 1, 1] %>% colMeans() %>% sqrt()
filtered_sds_slope <- filtered_covs[, , 2, 2] %>% colMeans() %>% sqrt()

forecast_df <- df %>%
  choose(month, IBM) %>%
  add_column(pred_mean = c(rep(NA, size(ts_train)), fc_means)) %>%
  add_column(pred_sd = c(rep(NA, size(ts_train)), fc_sds)) %>%
  add_column(smoothed_means_intercept = c(smoothed_means_intercept, rep(NA, n_forecast_steps))) %>%
  add_column(smoothed_means_slope = c(smoothed_means_slope, rep(NA, n_forecast_steps))) %>%
  add_column(smoothed_sds_intercept = c(smoothed_sds_intercept, rep(NA, n_forecast_steps))) %>%
  add_column(smoothed_sds_slope = c(smoothed_sds_slope, rep(NA, n_forecast_steps))) %>%
  add_column(filtered_means_intercept = c(filtered_means_intercept, rep(NA, n_forecast_steps))) %>%
  add_column(filtered_means_slope = c(filtered_means_slope, rep(NA, n_forecast_steps))) %>%
  add_column(filtered_sds_intercept = c(filtered_sds_intercept, rep(NA, n_forecast_steps))) %>%
  add_column(filtered_sds_slope = c(filtered_sds_slope, rep(NA, n_forecast_steps)))

So right here first are the forecasts. We’re utilizing the estimates returned from VI, however we might simply as effectively have used these from HMC – they’re almost indistinguishable. The identical goes for the filtering and smoothing estimates displayed beneath.

ggplot(forecast_df, aes(x = month, y = IBM)) +
  geom_line(coloration = "gray") +
  geom_line(aes(y = pred_mean), coloration = "cyan") +
  geom_ribbon(
    aes(ymin = pred_mean - 2 * pred_sd, ymax = pred_mean + 2 * pred_sd),
    alpha = 0.2,
    fill = "cyan"
  ) +
  theme(axis.title = element_blank())

12-point-ahead forecasts for IBM; posterior means +/- 2 standard deviations.

Figure 2: 12-point-ahead forecasts for IBM; posterior means +/- 2 commonplace deviations.

Smoothing estimates

Here are the smoothing estimates. The intercept (proven in orange) stays fairly steady over time, however we do see a pattern within the slope (displayed in inexperienced).

ggplot(forecast_df, aes(x = month, y = smoothed_means_intercept)) +
  geom_line(coloration = "orange") +
  geom_line(aes(y = smoothed_means_slope),
            coloration = "inexperienced") +
  geom_ribbon(
    aes(
      ymin = smoothed_means_intercept - 2 * smoothed_sds_intercept,
      ymax = smoothed_means_intercept + 2 * smoothed_sds_intercept
    ),
    alpha = 0.3,
    fill = "orange"
  ) +
  geom_ribbon(
    aes(
      ymin = smoothed_means_slope - 2 * smoothed_sds_slope,
      ymax = smoothed_means_slope + 2 * smoothed_sds_slope
    ),
    alpha = 0.1,
    fill = "inexperienced"
  ) +
  coord_cartesian(xlim = c(forecast_df$month[1], forecast_df$month[length(ts) - n_forecast_steps]))  +
  theme(axis.title = element_blank())

Smoothing estimates from the Kálmán filter. Green: coefficient for dependence on excess market returns (slope), orange: vector of ones (intercept).

Figure 3: Smoothing estimates from the Kálmán filter. Green: coefficient for dependence on extra market returns (slope), orange: vector of ones (intercept).

Filtering estimates

For comparability, listed below are the filtering estimates. Note that the y-axis extends additional up and down, so we will seize uncertainty higher:

ggplot(forecast_df, aes(x = month, y = filtered_means_intercept)) +
  geom_line(coloration = "orange") +
  geom_line(aes(y = filtered_means_slope),
            coloration = "inexperienced") +
  geom_ribbon(
    aes(
      ymin = filtered_means_intercept - 2 * filtered_sds_intercept,
      ymax = filtered_means_intercept + 2 * filtered_sds_intercept
    ),
    alpha = 0.3,
    fill = "orange"
  ) +
  geom_ribbon(
    aes(
      ymin = filtered_means_slope - 2 * filtered_sds_slope,
      ymax = filtered_means_slope + 2 * filtered_sds_slope
    ),
    alpha = 0.1,
    fill = "inexperienced"
  ) +
  coord_cartesian(ylim = c(-2, 2),
                  xlim = c(forecast_df$month[1], forecast_df$month[length(ts) - n_forecast_steps])) +
  theme(axis.title = element_blank())

Filtering estimates from the Kálmán filter. Green: coefficient for dependence on excess market returns (slope), orange: vector of ones (intercept).

Figure 4: Filtering estimates from the Kálmán filter. Green: coefficient for dependence on extra market returns (slope), orange: vector of ones (intercept).

So far, we’ve seen a full instance of time-series becoming, forecasting, and smoothing/filtering, in an thrilling setting one doesn’t encounter too usually: dynamic linear regression. What we haven’t seen as but is the additivity characteristic of DLMs, and the way it permits us to decompose a time sequence into its (theorized) constituents.
Let’s do that subsequent, in our second instance, anti-climactically making use of the iris of time sequence, AirPassengers. Any guesses what parts the mannequin would possibly presuppose?


AirPassengers.

Figure 5: AirPassengers.

Composition instance: AirPassengers

Libraries loaded, we put together the information for tfprobability:

The mannequin is a sum – cf. sts_sum – of a linear pattern and a seasonal element:

linear_trend <- ts %>% sts_local_linear_trend()
month-to-month <- ts %>% sts_seasonal(num_seasons = 12)
mannequin <- ts %>% sts_sum(parts = checklist(month-to-month, linear_trend))

Again, we might use VI in addition to MCMC to coach the mannequin. Here’s the VI method:

n_iterations <- 100
n_param_samples <- 50
n_forecast_samples <- 50

optimizer <- tf$compat$v1$prepare$AdamOptimizer(0.1)

fit_vi <-
  operate(ts,
           ts_train,
           mannequin,
           n_iterations,
           n_param_samples,
           n_forecast_steps,
           n_forecast_samples) {
    loss_and_dists <-
      ts_train %>% sts_build_factored_variational_loss(mannequin = mannequin)
    variational_loss <- loss_and_dists[[1]]
    train_op <- optimizer$decrease(variational_loss)
    
    with (tf$Session() %as% sess,  {
      sess$run(tf$compat$v1$global_variables_initializer())
      for (step in 1:n_iterations) {
        res <- sess$run(train_op)
        loss <- sess$run(variational_loss)
        if (step %% 1 == 0)
          cat("Loss: ", as.numeric(loss), "n")
      }
      variational_distributions <- loss_and_dists[[2]]
      posterior_samples <-
        Map(
          operate(d)
            d %>% tfd_sample(n_param_samples),
          variational_distributions %>% reticulate::py_to_r() %>% unname()
        )
      forecast_dists <-
        ts_train %>% sts_forecast(mannequin, posterior_samples, n_forecast_steps)
      fc_means <- forecast_dists %>% tfd_mean()
      fc_sds <- forecast_dists %>% tfd_stddev()
      
      c(posterior_samples,
        fc_means,
        fc_sds) %<-%
        sess$run(checklist(posterior_samples,
                      fc_means,
                      fc_sds))
    })
    
    checklist(variational_distributions,
         posterior_samples,
         fc_means[, 1],
         fc_sds[, 1])
  }

c(param_distributions,
  param_samples,
  fc_means,
  fc_sds) %<-% fit_vi(
    ts,
    ts_train,
    mannequin,
    n_iterations,
    n_param_samples,
    n_forecast_steps,
    n_forecast_samples
  )

For brevity, we haven’t computed smoothed and/or filtered estimates for the general mannequin. In this instance, this being a sum mannequin, we wish to present one thing else as a substitute: the way in which it decomposes into parts.

But first, the forecasts:

forecast_df <- df %>%
  add_column(pred_mean = c(rep(NA, size(ts_train)), fc_means)) %>%
  add_column(pred_sd = c(rep(NA, size(ts_train)), fc_sds))


ggplot(forecast_df, aes(x = month, y = n)) +
  geom_line(coloration = "gray") +
  geom_line(aes(y = pred_mean), coloration = "cyan") +
  geom_ribbon(
    aes(ymin = pred_mean - 2 * pred_sd, ymax = pred_mean + 2 * pred_sd),
    alpha = 0.2,
    fill = "cyan"
  ) +
  theme(axis.title = element_blank())

AirPassengers, 12-months-ahead forecast.

Figure 6: AirPassengers, 12-months-ahead forecast.

A name to sts_decompose_by_component yields the (centered) parts, a linear pattern and a seasonal issue:

component_dists <-
  ts_train %>% sts_decompose_by_component(mannequin = mannequin, parameter_samples = param_samples)

seasonal_effect_means <- component_dists[[1]] %>% tfd_mean()
seasonal_effect_sds <- component_dists[[1]] %>% tfd_stddev()
linear_effect_means <- component_dists[[2]] %>% tfd_mean()
linear_effect_sds <- component_dists[[2]] %>% tfd_stddev()

with(tf$Session() %as% sess, {
  c(
    seasonal_effect_means,
    seasonal_effect_sds,
    linear_effect_means,
    linear_effect_sds
  ) %<-% sess$run(
    checklist(
      seasonal_effect_means,
      seasonal_effect_sds,
      linear_effect_means,
      linear_effect_sds
    )
  )
})

components_df <- forecast_df %>%
  add_column(seasonal_effect_means = c(seasonal_effect_means, rep(NA, n_forecast_steps))) %>%
  add_column(seasonal_effect_sds = c(seasonal_effect_sds, rep(NA, n_forecast_steps))) %>%
  add_column(linear_effect_means = c(linear_effect_means, rep(NA, n_forecast_steps))) %>%
  add_column(linear_effect_sds = c(linear_effect_sds, rep(NA, n_forecast_steps)))

ggplot(components_df, aes(x = month, y = n)) +
  geom_line(aes(y = seasonal_effect_means), coloration = "orange") +
  geom_ribbon(
    aes(
      ymin = seasonal_effect_means - 2 * seasonal_effect_sds,
      ymax = seasonal_effect_means + 2 * seasonal_effect_sds
    ),
    alpha = 0.2,
    fill = "orange"
  ) +
  theme(axis.title = element_blank()) +
  geom_line(aes(y = linear_effect_means), coloration = "inexperienced") +
  geom_ribbon(
    aes(
      ymin = linear_effect_means - 2 * linear_effect_sds,
      ymax = linear_effect_means + 2 * linear_effect_sds
    ),
    alpha = 0.2,
    fill = "inexperienced"
  ) +
  theme(axis.title = element_blank())

AirPassengers, decomposition into a linear trend and a seasonal component (both centered).

Figure 7: AirPassengers, decomposition right into a linear pattern and a seasonal element (each centered).

Wrapping up

We’ve seen how with DLMs, there’s a bunch of fascinating stuff you are able to do – other than acquiring forecasts, which in all probability would be the final objective in most purposes – : You can examine the smoothed and the filtered estimates from the Kálmán filter, and you’ll decompose a mannequin into its posterior parts. A very engaging mannequin is dynamic linear regression, featured in our first instance, which permits us to acquire regression coefficients that modify over time.

This put up confirmed the best way to accomplish this with tfprobability. As of at this time, TensorFlow (and thus, TensorFlow Probability) is in a state of considerable inner adjustments, with desirous to turn out to be the default execution mode very quickly. Concurrently, the superior TensorFlow Probability improvement group are including new and thrilling options daily. Consequently, this put up is snapshot capturing the best way to finest accomplish these targets now: If you’re studying this just a few months from now, chances are high that what’s work in progress now can have turn out to be a mature methodology by then, and there could also be sooner methods to achieve the identical targets. At the speed TFP is evolving, we’re excited for the issues to return!

Berndt, R. 1991. The Practice of Econometrics. Addison-Wesley.

Murphy, Kevin. 2012. Machine Learning: A Probabilistic Perspective. MIT Press.

Petris, Giovanni, sonia Petrone, and Patrizia Campagnoli. 2009. Dynamic Linear Models with r. Springer.

LEAVE A REPLY

Please enter your comment!
Please enter your name here