[ad_1]
Last Updated on November 15, 2022
Derivatives are some of the elementary ideas in calculus. They describe how adjustments within the variable inputs have an effect on the operate outputs. The goal of this text is to offer a high-level introduction to calculating derivatives in PyTorch for many who are new to the framework. PyTorch gives a handy solution to calculate derivatives for user-defined features.
While we at all times should cope with backpropagation (an algorithm identified to be the spine of a neural community) in neural networks, which optimizes the parameters to reduce the error with the intention to obtain larger classification accuracy; ideas discovered on this article can be utilized in later posts on deep studying for picture processing and different laptop imaginative and prescient issues.
After going via this tutorial, you’ll study:
- How to calculate derivatives in PyTorch.
- How to make use of autograd in PyTorch to carry out auto differentiation on tensors.
- About the computation graph that entails completely different nodes and leaves, permitting you to calculate the gradients in a easy doable method (utilizing the chain rule).
- How to calculate partial derivatives in PyTorch.
- How to implement the spinoff of features with respect to a number of values.
Let’s get began.

Calculating Derivatives in PyTorch
Picture by Jossuha Théophile. Some rights reserved.
Differentiation in Autograd
The autograd – an auto differentiation module in PyTorch – is used to calculate the derivatives and optimize the parameters in neural networks. It is meant primarily for gradient computations.
Before we begin, let’s load up some needed libraries we’ll use on this tutorial.
|
import matplotlib.pyplot as plt import torch |
Now, let’s use a easy tensor and set the requires_grad parameter to true. This permits us to carry out computerized differentiation and lets PyTorch consider the derivatives utilizing the given worth which, on this case, is 3.0.
|
x = torch.tensor(3.0, requires_grad = True) print(“making a tensor x: “, x) |
|
making a tensor x: tensor(3., requires_grad=True) |
We’ll use a easy equation $y=3x^2$ for example and take the spinoff with respect to variable x. So, let’s create one other tensor in response to the given equation. Also, we’ll apply a neat methodology .backward on the variable y that varieties acyclic graph storing the computation historical past, and consider the consequence with .grad for the given worth.
|
y = 3 * x ** 2 print(“Result of the equation is: “, y) y.backward() print(“Dervative of the equation at x = 3 is: “, x.grad) |
|
Result of the equation is: tensor(27., grad_fn=<MulBackward0>) Dervative of the equation at x = 3 is: tensor(18.) |
As you possibly can see, we’ve got obtained a worth of 18, which is right.
Computational Graph
PyTorch generates derivatives by constructing a backwards graph behind the scenes, whereas tensors and backwards features are the graph’s nodes. In a graph, PyTorch computes the spinoff of a tensor relying on whether or not it’s a leaf or not.
PyTorch won’t consider a tensor’s spinoff if its leaf attribute is about to True. We gained’t go into a lot element about how the backwards graph is created and utilized, as a result of the objective right here is to offer you a high-level information of how PyTorch makes use of the graph to calculate derivatives.
So, let’s examine how the tensors x and y look internally as soon as they’re created. For x:
|
print(‘information attribute of the tensor:’,x.information) print(‘grad attribute of the tensor::’,x.grad) print(‘grad_fn attribute of the tensor::’,x.grad_fn) print(“is_leaf attribute of the tensor::”,x.is_leaf) print(“requires_grad attribute of the tensor::”,x.requires_grad) |
|
information attribute of the tensor: tensor(3.) grad attribute of the tensor:: tensor(18.) grad_fn attribute of the tensor:: None is_leaf attribute of the tensor:: True requires_grad attribute of the tensor:: True |
and for y:
|
print(‘information attribute of the tensor:’,y.information) print(‘grad attribute of the tensor:’,y.grad) print(‘grad_fn attribute of the tensor:’,y.grad_fn) print(“is_leaf attribute of the tensor:”,y.is_leaf) print(“requires_grad attribute of the tensor:”,y.requires_grad) |
|
print(‘information attribute of the tensor:’,y.information) print(‘grad attribute of the tensor:’,y.grad) print(‘grad_fn attribute of the tensor:’,y.grad_fn) print(“is_leaf attribute of the tensor:”,y.is_leaf) print(“requires_grad attribute of the tensor:”,y.requires_grad) |
As you possibly can see, every tensor has been assigned with a selected set of attributes.
The information attribute shops the tensor’s information whereas the grad_fn attribute tells concerning the node within the graph. Likewise, the .grad attribute holds the results of the spinoff. Now that you’ve learnt some fundamentals concerning the autograd and computational graph in PyTorch, let’s take a bit extra difficult equation $y=6x^2+2x+4$ and calculate the spinoff. The spinoff of the equation is given by:
$$frac{dy}{dx} = 12x+2$$
Evaluating the spinoff at $x = 3$,
$$left.frac{dy}{dx}rightvert_{x=3} = 12times 3+2 = 38$$
Now, let’s see how PyTorch does that,
|
x = torch.tensor(3.0, requires_grad = True) y = 6 * x ** 2 + 2 * x + 4 print(“Result of the equation is: “, y) y.backward() print(“Derivative of the equation at x = 3 is: “, x.grad) |
|
Result of the equation is: tensor(64., grad_fn=<AddBackward0>) Derivative of the equation at x = 3 is: tensor(38.) |
The spinoff of the equation is 38, which is right.
Implementing Partial Derivatives of Functions
PyTorch additionally permits us to calculate partial derivatives of features. For instance, if we’ve got to use partial derivation to the next operate,
$$f(u,v) = u^3+v^2+4uv$$
Its spinoff with respect to $u$ is,
$$frac{partial f}{partial u} = 3u^2 + 4v$$
Similarly, the spinoff with respect to $v$ can be,
$$frac{partial f}{partial v} = 2v + 4u$$
Now, let’s do it the PyTorch approach, the place $u = 3$ and $v = 4$.
We’ll create u, v and f tensors and apply the .backward attribute on f with the intention to compute the spinoff. Finally, we’ll consider the spinoff utilizing the .grad with respect to the values of u and v.
|
u = torch.tensor(3., requires_grad=True) v = torch.tensor(4., requires_grad=True)
f = u**3 + v**2 + 4*u*v
print(u) print(v) print(f)
f.backward() print(“Partial spinoff with respect to u: “, u.grad) print(“Partial spinoff with respect to v: “, v.grad) |
|
tensor(3., requires_grad=True) tensor(4., requires_grad=True) tensor(91., grad_fn=<AddBackward0>) Partial spinoff with respect to u: tensor(43.) Partial spinoff with respect to v: tensor(20.) |
Derivative of Functions with Multiple Values
What if we’ve got a operate with a number of values and we have to calculate the spinoff with respect to its a number of values? For this, we’ll make use of the sum attribute to (1) produce a scalar-valued operate, after which (2) take the spinoff. This is how we will see the ‘function vs. derivative’ plot:
|
# compute the spinoff of the operate with a number of values x = torch.linspace(–20, 20, 20, requires_grad = True) Y = x ** 2 y = torch.sum(Y) y.backward()
# ploting the operate and spinoff function_line, = plt.plot(x.detach().numpy(), Y.detach().numpy(), label = ‘Function’) function_line.set_color(“purple”) derivative_line, = plt.plot(x.detach().numpy(), x.grad.detach().numpy(), label = ‘Derivative’) derivative_line.set_color(“inexperienced”) plt.xlabel(‘x’) plt.legend() plt.present() |
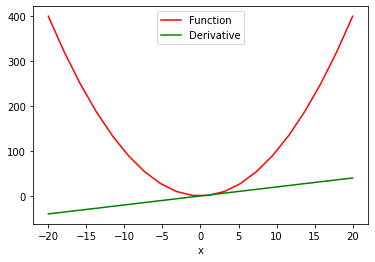
In the 2 plot() operate above, we extract the values from PyTorch tensors so we will visualize them. The .detach methodology doesn’t permit the graph to additional monitor the operations. This makes it straightforward for us to transform a tensor to a numpy array.
Summary
In this tutorial, you discovered the best way to implement derivatives on numerous features in PyTorch.
Particularly, you discovered:
- How to calculate derivatives in PyTorch.
- How to make use of autograd in PyTorch to carry out auto differentiation on tensors.
- About the computation graph that entails completely different nodes and leaves, permitting you to calculate the gradients in a easy doable method (utilizing the chain rule).
- How to calculate partial derivatives in PyTorch.
- How to implement the spinoff of features with respect to a number of values.
