[ad_1]
TLDR: We suggest the uneven licensed robustness drawback, which requires licensed robustness for just one class and displays real-world adversarial situations. This centered setting permits us to introduce feature-convex classifiers, which produce closed-form and deterministic licensed radii on the order of milliseconds.

Figure 1. Illustration of feature-convex classifiers and their certification for sensitive-class inputs. This structure composes a Lipschitz-continuous function map $varphi$ with a discovered convex perform $g$. Since $g$ is convex, it’s globally underapproximated by its tangent aircraft at $varphi(x)$, yielding licensed norm balls within the function house. Lipschitzness of $varphi$ then yields appropriately scaled certificates within the authentic enter house.
Despite their widespread utilization, deep studying classifiers are acutely susceptible to adversarial examples: small, human-imperceptible picture perturbations that idiot machine studying fashions into misclassifying the modified enter. This weak spot severely undermines the reliability of safety-critical processes that incorporate machine studying. Many empirical defenses in opposition to adversarial perturbations have been proposed—typically solely to be later defeated by stronger assault methods. We due to this fact concentrate on certifiably sturdy classifiers, which give a mathematical assure that their prediction will stay fixed for an $ell_p$-norm ball round an enter.
Conventional licensed robustness strategies incur a spread of drawbacks, together with nondeterminism, gradual execution, poor scaling, and certification in opposition to just one assault norm. We argue that these points could be addressed by refining the licensed robustness drawback to be extra aligned with sensible adversarial settings.
The Asymmetric Certified Robustness Problem
Current certifiably sturdy classifiers produce certificates for inputs belonging to any class. For many real-world adversarial purposes, that is unnecessarily broad. Consider the illustrative case of somebody composing a phishing rip-off e mail whereas making an attempt to keep away from spam filters. This adversary will all the time try to idiot the spam filter into pondering that their spam e mail is benign—by no means conversely. In different phrases, the attacker is solely trying to induce false negatives from the classifier. Similar settings embrace malware detection, pretend information flagging, social media bot detection, medical insurance coverage claims filtering, monetary fraud detection, phishing web site detection, and lots of extra.
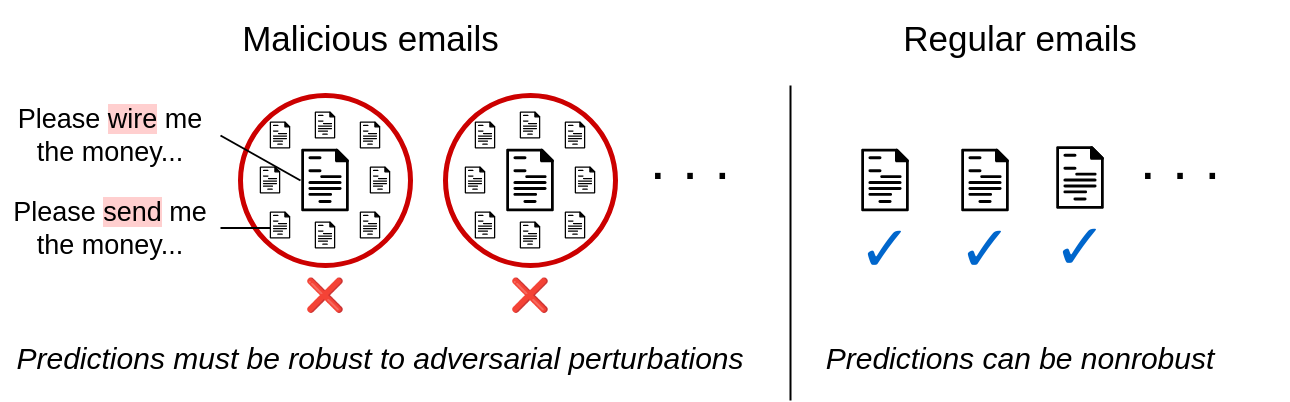
Figure 2. Asymmetric robustness in e mail filtering. Practical adversarial settings typically require licensed robustness for just one class.
These purposes all contain a binary classification setting with one delicate class that an adversary is trying to keep away from (e.g., the “spam email” class). This motivates the issue of uneven licensed robustness, which goals to supply certifiably sturdy predictions for inputs within the delicate class whereas sustaining a excessive clear accuracy for all different inputs. We present a extra formal drawback assertion in the primary textual content.
Feature-convex classifiers
We suggest feature-convex neural networks to deal with the uneven robustness drawback. This structure composes a easy Lipschitz-continuous function map ${varphi: mathbb{R}^d to mathbb{R}^q}$ with a discovered Input-Convex Neural Network (ICNN) ${g: mathbb{R}^q to mathbb{R}}$ (Figure 1). ICNNs implement convexity from the enter to the output logit by composing ReLU nonlinearities with nonnegative weight matrices. Since a binary ICNN resolution area consists of a convex set and its complement, we add the precomposed function map $varphi$ to allow nonconvex resolution areas.
Feature-convex classifiers allow the quick computation of sensitive-class licensed radii for all $ell_p$-norms. Using the truth that convex capabilities are globally underapproximated by any tangent aircraft, we will acquire an authorized radius within the intermediate function house. This radius is then propagated to the enter house by Lipschitzness. The uneven setting right here is vital, as this structure solely produces certificates for the positive-logit class $g(varphi(x)) > 0$.
The ensuing $ell_p$-norm licensed radius components is especially elegant:
[r_p(x) = frac{ color{blue}{g(varphi(x))} } { mathrm{Lip}_p(varphi) color{red}{| nabla g(varphi(x)) | _{p,*}}}.]
The non-constant phrases are simply interpretable: the radius scales proportionally to the classifier confidence and inversely to the classifier sensitivity. We consider these certificates throughout a spread of datasets, reaching aggressive $ell_1$ certificates and comparable $ell_2$ and $ell_{infty}$ certificates—regardless of different strategies usually tailoring for a selected norm and requiring orders of magnitude extra runtime.
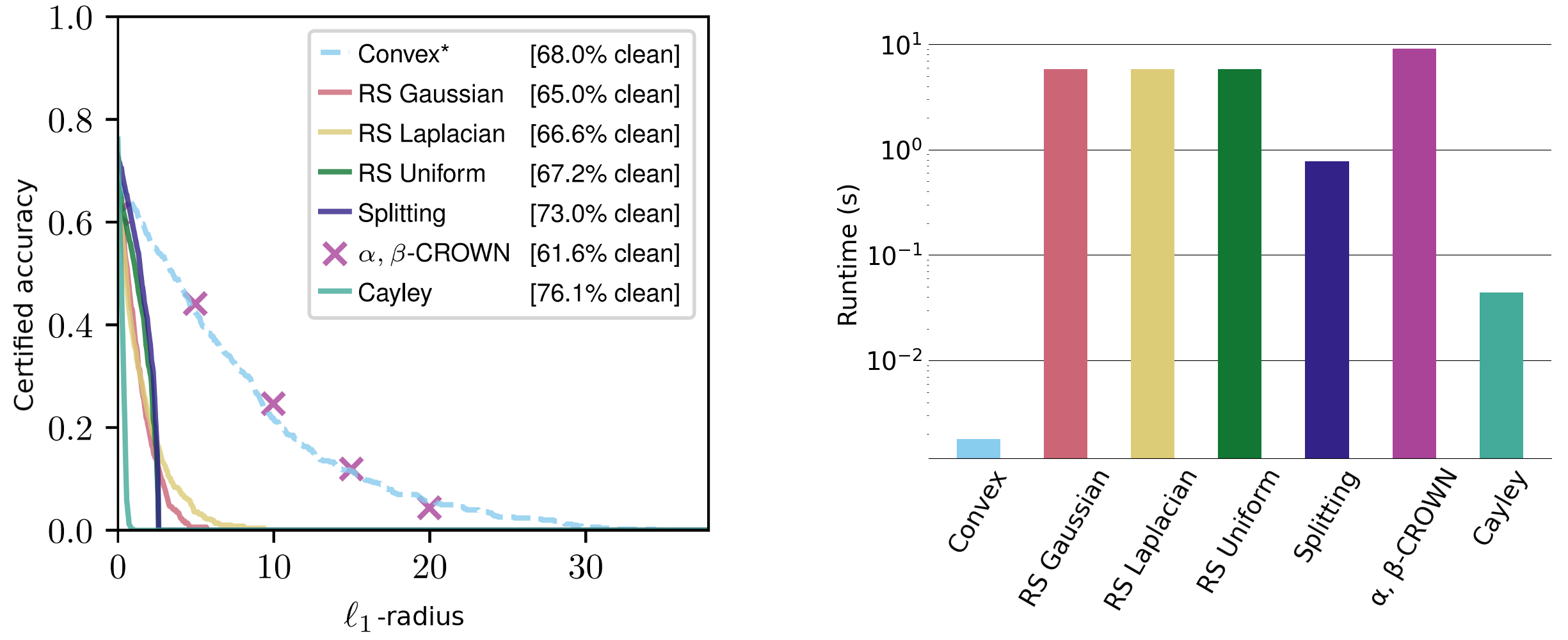
Figure 3. Sensitive class licensed radii on the CIFAR-10 cats vs canines dataset for the $ell_1$-norm. Runtimes on the proper are averaged over $ell_1$, $ell_2$, and $ell_{infty}$-radii (observe the log scaling).
Our certificates maintain for any $ell_p$-norm and are closed kind and deterministic, requiring only one forwards and backwards cross per enter. These are computable on the order of milliseconds and scale properly with community dimension. For comparability, present state-of-the-art strategies resembling randomized smoothing and interval sure propagation usually take a number of seconds to certify even small networks. Randomized smoothing strategies are additionally inherently nondeterministic, with certificates that simply maintain with excessive likelihood.
Theoretical promise
While preliminary outcomes are promising, our theoretical work suggests that there’s vital untapped potential in ICNNs, even with no function map. Despite binary ICNNs being restricted to studying convex resolution areas, we show that there exists an ICNN that achieves excellent coaching accuracy on the CIFAR-10 cats-vs-dogs dataset.
Fact. There exists an input-convex classifier which achieves excellent coaching accuracy for the CIFAR-10 cats-versus-dogs dataset.
However, our structure achieves simply $73.4%$ coaching accuracy with no function map. While coaching efficiency doesn’t indicate check set generalization, this end result means that ICNNs are at the very least theoretically able to attaining the trendy machine studying paradigm of overfitting to the coaching dataset. We thus pose the next open drawback for the sector.
Open drawback. Learn an input-convex classifier which achieves excellent coaching accuracy for the CIFAR-10 cats-versus-dogs dataset.
Conclusion
We hope that the uneven robustness framework will encourage novel architectures that are certifiable on this extra centered setting. Our feature-convex classifier is one such structure and offers quick, deterministic licensed radii for any $ell_p$-norm. We additionally pose the open drawback of overfitting the CIFAR-10 cats vs canines coaching dataset with an ICNN, which we present is theoretically attainable.
This publish is predicated on the next paper:
Asymmetric Certified Robustness through Feature-Convex Neural Networks
Samuel Pfrommer,
Brendon G. Anderson,
Julien Piet,
Somayeh Sojoudi,
thirty seventh Conference on Neural Information Processing Systems (NeurIPS 2023).
Further particulars can be found on arXiv and GitHub. If our paper evokes your work, please think about citing it with:
@inproceedings{
pfrommer2023asymmetric,
title={Asymmetric Certified Robustness through Feature-Convex Neural Networks},
creator={Samuel Pfrommer and Brendon G. Anderson and Julien Piet and Somayeh Sojoudi},
booktitle={Thirty-seventh Conference on Neural Information Processing Systems},
12 months={2023}
}
[ad_2]
