[ad_1]
Figure 1: stepwise habits in self-supervised studying. When coaching widespread SSL algorithms, we discover that the loss descends in a stepwise trend (high left) and the realized embeddings iteratively improve in dimensionality (backside left). Direct visualization of embeddings (proper; high three PCA instructions proven) confirms that embeddings are initially collapsed to a degree, which then expands to a 1D manifold, a 2D manifold, and past concurrently with steps within the loss.
It is extensively believed that deep studying’s gorgeous success is due partly to its skill to find and extract helpful representations of advanced knowledge. Self-supervised studying (SSL) has emerged as a number one framework for studying these representations for pictures straight from unlabeled knowledge, just like how LLMs be taught representations for language straight from web-scraped textual content. Yet regardless of SSL’s key position in state-of-the-art fashions corresponding to CLIP and MidJourney, elementary questions like “what are self-supervised image systems really learning?” and “how does that learning actually occur?” lack primary solutions.
Our current paper (to look at ICML 2023) presents what we recommend is the primary compelling mathematical image of the coaching technique of large-scale SSL strategies. Our simplified theoretical mannequin, which we clear up precisely, learns points of the information in a sequence of discrete, well-separated steps. We then reveal that this habits will be noticed within the wild throughout many present state-of-the-art programs.
This discovery opens new avenues for bettering SSL strategies, and permits a complete vary of recent scientific questions that, when answered, will present a strong lens for understanding a few of at present’s most necessary deep studying programs.
Background
We focus right here on joint-embedding SSL strategies — a superset of contrastive strategies — which be taught representations that obey view-invariance standards. The loss operate of those fashions features a time period implementing matching embeddings for semantically equal “views” of a picture. Remarkably, this easy strategy yields highly effective representations on picture duties even when views are so simple as random crops and shade perturbations.
Theory: stepwise studying in SSL with linearized fashions
We first describe an precisely solvable linear mannequin of SSL through which each the coaching trajectories and remaining embeddings will be written in closed type. Notably, we discover that illustration studying separates right into a sequence of discrete steps: the rank of the embeddings begins small and iteratively will increase in a stepwise studying course of.
The principal theoretical contribution of our paper is to precisely clear up the coaching dynamics of the Barlow Twins loss operate beneath gradient circulate for the particular case of a linear mannequin (mathbf{f}(mathbf{x}) = mathbf{W} mathbf{x}). To sketch our findings right here, we discover that, when initialization is small, the mannequin learns representations composed exactly of the top-(d) eigendirections of the featurewise cross-correlation matrix (boldsymbol{Gamma} equiv mathbb{E}_{mathbf{x},mathbf{x}’} [ mathbf{x} mathbf{x}’^T ]). What’s extra, we discover that these eigendirections are realized separately in a sequence of discrete studying steps at instances decided by their corresponding eigenvalues. Figure 2 illustrates this studying course of, exhibiting each the expansion of a brand new course within the represented operate and the ensuing drop within the loss at every studying step. As an additional bonus, we discover a closed-form equation for the ultimate embeddings realized by the mannequin at convergence.
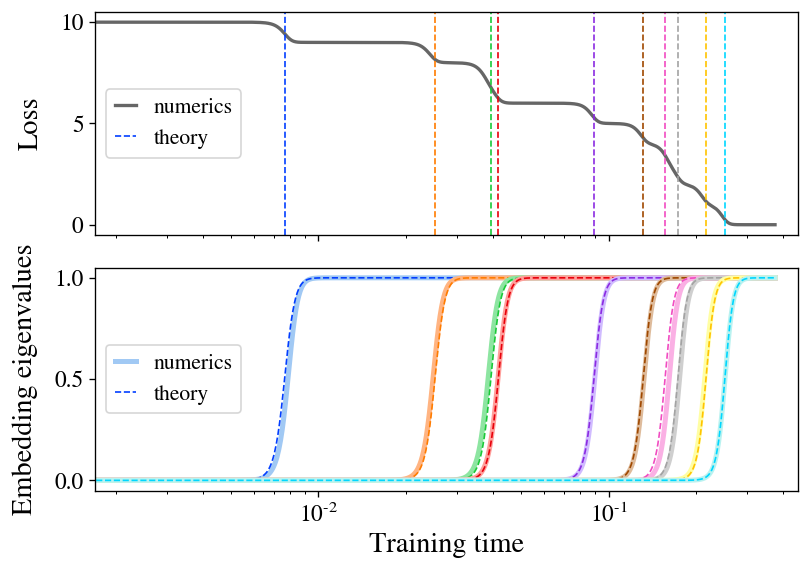
Figure 2: stepwise studying seems in a linear mannequin of SSL. We prepare a linear mannequin with the Barlow Twins loss on a small pattern of CIFAR-10. The loss (high) descends in a staircase trend, with step instances well-predicted by our principle (dashed strains). The embedding eigenvalues (backside) spring up separately, carefully matching principle (dashed curves).
Our discovering of stepwise studying is a manifestation of the broader idea of spectral bias, which is the commentary that many studying programs with roughly linear dynamics preferentially be taught eigendirections with increased eigenvalue. This has lately been well-studied within the case of normal supervised studying, the place it’s been discovered that higher-eigenvalue eigenmodes are realized quicker throughout coaching. Our work finds the analogous outcomes for SSL.
The motive a linear mannequin deserves cautious examine is that, as proven through the “neural tangent kernel” (NTK) line of labor, sufficiently broad neural networks even have linear parameterwise dynamics. This reality is adequate to increase our answer for a linear mannequin to broad neural nets (or actually to arbitrary kernel machines), through which case the mannequin preferentially learns the highest (d) eigendirections of a specific operator associated to the NTK. The examine of the NTK has yielded many insights into the coaching and generalization of even nonlinear neural networks, which is a clue that maybe a number of the insights we’ve gleaned would possibly switch to practical instances.
Experiment: stepwise studying in SSL with ResNets
As our principal experiments, we prepare a number of main SSL strategies with full-scale ResNet-50 encoders and discover that, remarkably, we clearly see this stepwise studying sample even in practical settings, suggesting that this habits is central to the training habits of SSL.
To see stepwise studying with ResNets in practical setups, all we now have to do is run the algorithm and monitor the eigenvalues of the embedding covariance matrix over time. In apply, it helps spotlight the stepwise habits to additionally prepare from smaller-than-normal parameter-wise initialization and prepare with a small studying fee, so we’ll use these modifications within the experiments we discuss right here and focus on the usual case in our paper.
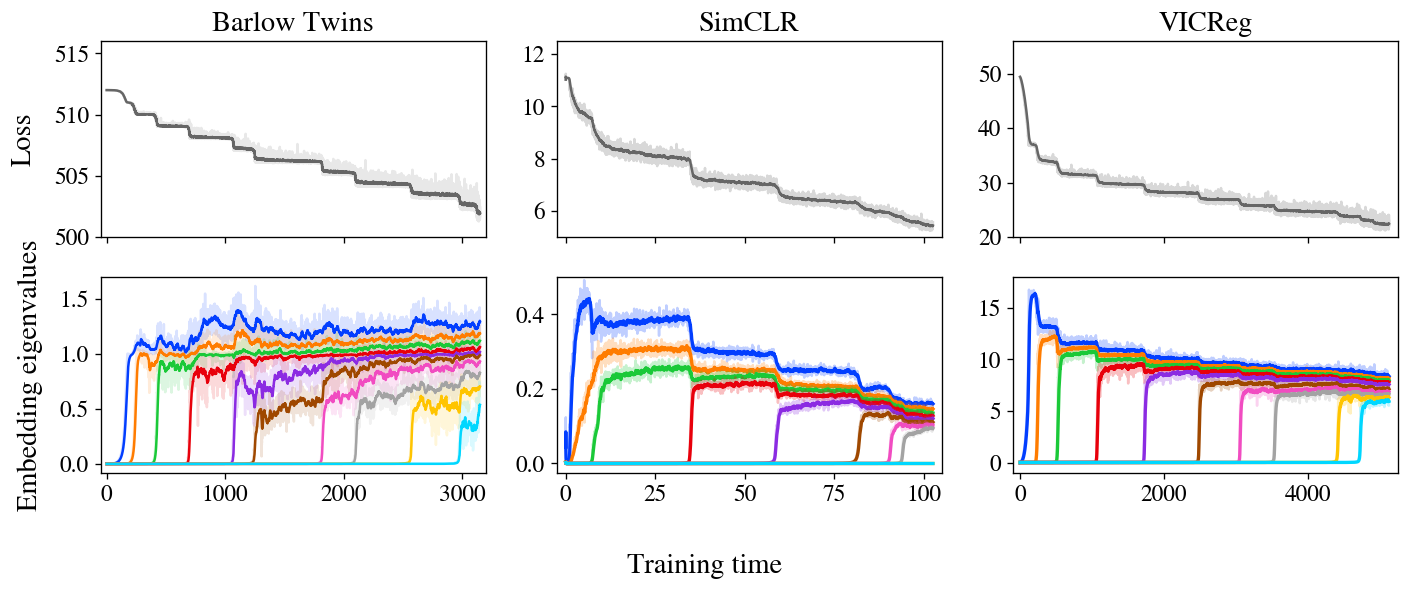
Figure 3: stepwise studying is obvious in Barlow Twins, SimCLR, and VICReg. The loss and embeddings of all three strategies show stepwise studying, with embeddings iteratively growing in rank as predicted by our mannequin.
Figure 3 exhibits losses and embedding covariance eigenvalues for 3 SSL strategies — Barlow Twins, SimCLR, and VICReg — skilled on the STL-10 dataset with customary augmentations. Remarkably, all three present very clear stepwise studying, with loss lowering in a staircase curve and one new eigenvalue arising from zero at every subsequent step. We additionally present an animated zoom-in on the early steps of Barlow Twins in Figure 1.
It’s value noting that, whereas these three strategies are moderately totally different at first look, it’s been suspected in folklore for a while that they’re doing one thing related beneath the hood. In explicit, these and different joint-embedding SSL strategies all obtain related efficiency on benchmark duties. The problem, then, is to establish the shared habits underlying these assorted strategies. Much prior theoretical work has centered on analytical similarities of their loss capabilities, however our experiments recommend a distinct unifying precept: SSL strategies all be taught embeddings one dimension at a time, iteratively including new dimensions so as of salience.
In a final incipient however promising experiment, we examine the actual embeddings realized by these strategies with theoretical predictions computed from the NTK after coaching. We not solely discover good settlement between principle and experiment inside every methodology, however we additionally examine throughout strategies and discover that totally different strategies be taught related embeddings, including additional assist to the notion that these strategies are in the end doing related issues and will be unified.
Why it issues
Our work paints a primary theoretical image of the method by which SSL strategies assemble realized representations over the course of coaching. Now that we now have a principle, what can we do with it? We see promise for this image to each help the apply of SSL from an engineering standpoint and to allow higher understanding of SSL and probably illustration studying extra broadly.
On the sensible facet, SSL fashions are famously gradual to coach in comparison with supervised coaching, and the explanation for this distinction isn’t recognized. Our image of coaching means that SSL coaching takes a very long time to converge as a result of the later eigenmodes have very long time constants and take a very long time to develop considerably. If that image’s proper, dashing up coaching can be so simple as selectively focusing gradient on small embedding eigendirections in an try to tug them as much as the extent of the others, which will be accomplished in precept with only a easy modification to the loss operate or the optimizer. We focus on these prospects in additional element in our paper.
On the scientific facet, the framework of SSL as an iterative course of permits one to ask many questions on the person eigenmodes. Are those realized first extra helpful than those realized later? How do totally different augmentations change the realized modes, and does this rely on the particular SSL methodology used? Can we assign semantic content material to any (subset of) eigenmodes? (For instance, we’ve observed that the primary few modes realized generally characterize extremely interpretable capabilities like a picture’s common hue and saturation.) If different types of illustration studying converge to related representations — a reality which is well testable — then solutions to those questions might have implications extending to deep studying extra broadly.
All thought of, we’re optimistic in regards to the prospects of future work within the space. Deep studying stays a grand theoretical thriller, however we consider our findings right here give a helpful foothold for future research into the training habits of deep networks.
This put up is predicated on the paper “On the Stepwise Nature of Self-Supervised Learning”, which is joint work with Maksis Knutins, Liu Ziyin, Daniel Geisz, and Joshua Albrecht. This work was performed with Generally Intelligent the place Jamie Simon is a Research Fellow. This blogpost is cross-posted right here. We’d be delighted to subject your questions or feedback.
