When quantum computer systems have been first proposed, they have been hoped to be a technique to higher perceive the quantum world. With a so-called “quantum simulator,” one may engineer a quantum pc to analyze how numerous quantum phenomena come up, together with these which are intractable to simulate with a classical pc.
But making a helpful quantum simulator has been a problem. Until now, quantum simulations with superconducting qubits have predominantly been used to confirm pre-existing theoretical predictions and have not often explored or found new phenomena. Only a number of experiments with trapped ions or chilly atoms have revealed new insights. Superconducting qubits, though they’re one of many foremost candidates for common quantum computing and have demonstrated computational capabilities past classical attain, have up to now not delivered on their potential for discovery.
In “Formation of Robust Bound States of Interacting Photons”, revealed in Nature, we describe a beforehand unpredicted phenomenon first found via experimental investigation. First, we current the experimental affirmation of the theoretical prediction of the existence of a composite particle of interacting photons, or a sure state, utilizing the Google Sycamore quantum processor. Second, whereas learning this technique, we found that though one would possibly guess the sure states to be fragile, they continue to be strong to perturbations that we anticipated to have in any other case destroyed them. Not solely does this open the potential of designing methods that leverage interactions between photons, it additionally marks a step ahead in using superconducting quantum processors to make new scientific discoveries by simulating non-equilibrium quantum dynamics.
Overview
Photons, or quanta of electromagnetic radiation like mild and microwaves, sometimes don’t work together. For instance, two intersecting flashlight beams will cross via each other undisturbed. In many purposes, like telecommunications, the weak interactions of photons is a useful characteristic. For different purposes, resembling computer systems based mostly on mild, the dearth of interactions between photons is a shortcoming.
In a quantum processor, the qubits host microwave photons, which may be made to work together via two-qubit operations. This permits us to simulate the XXZ mannequin, which describes the conduct of interacting photons. Importantly, this is without doubt one of the few examples of integrable fashions, i.e., one with a excessive diploma of symmetry, which tremendously reduces its complexity. When we implement the XXZ mannequin on the Sycamore processor, we observe one thing putting: the interactions drive the photons into bundles often known as sure states.
Using this well-understood mannequin as a place to begin, we then push the examine right into a less-understood regime. We break the excessive degree of symmetries displayed within the XXZ mannequin by including further websites that may be occupied by the photons, making the system now not integrable. While this nonintegrable regime is anticipated to exhibit chaotic conduct the place sure states dissolve into their regular, solitary selves, we as an alternative discover that they survive!
Bound Photons
To engineer a system that may assist the formation of sure states, we examine a hoop of superconducting qubits that host microwave photons. If a photon is current, the worth of the qubit is “1”, and if not, the worth is “0”. Through the so-called “fSim” quantum gate, we join neighboring websites, permitting the photons to hop round and work together with different photons on the nearest-neighboring websites.
 |
| Superconducting qubits may be occupied or unoccupied with microwave photons. The “fSim” gate operation permits photons to hop and work together with one another. The corresponding unitary evolution has a hopping time period between two websites (orange) and an interplay time period similar to an added part when two adjoining websites are occupied by a photon. |
 |
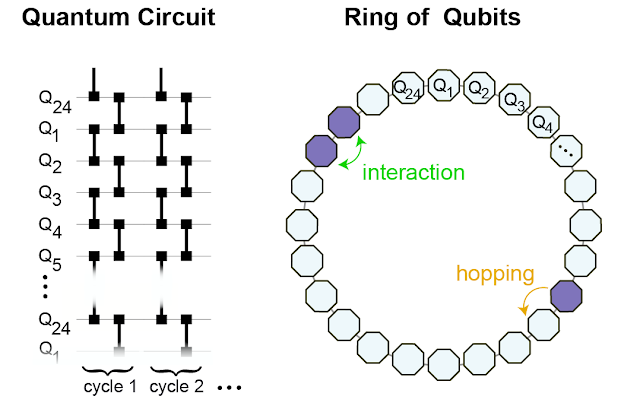| We implement the fSim gate between neighboring qubits (left) to successfully kind a hoop of 24 interconnected qubits on which we simulate the conduct of the interacting photons (proper). |
The interactions between the photons have an effect on their so-called “phase.” This part retains observe of the oscillation of the photon’s wavefunction. When the photons are non-interacting, their part accumulation is quite uninteresting. Like a well-rehearsed choir, they’re all in sync with each other. In this case, a photon that was initially subsequent to a different photon can hop away from its neighbor with out getting out of sync. Just as each particular person within the choir contributes to the music, each doable path the photon can take contributes to the photon’s total wavefunction. A gaggle of photons initially clustered on neighboring websites will evolve right into a superposition of all doable paths every photon might need taken.
When photons work together with their neighbors, that is now not the case. If one photon hops away from its neighbor, its fee of part accumulation modifications, changing into out of sync with its neighbors. All paths through which the photons cut up aside overlap, resulting in damaging interference. It can be like every choir member singing at their very own tempo — the music itself will get washed out, changing into unattainable to discern via the din of the person singers. Among all of the doable configuration paths, the one doable state of affairs that survives is the configuration through which all photons stay clustered collectively in a sure state. This is why interplay can improve and result in the formation of a sure state: by suppressing all different potentialities through which photons will not be sure collectively.
 |
| Left: Evolution of interacting photons forming a sure state. Right: Time goes from left to proper, every path represents one of many paths that may break the 2-photon bonded state. Due to interactions, these paths intervene destructively, stopping the photons from splitting aside. |
 |
| Occupation likelihood versus gate cycle, or discrete time step, for n-photon sure states. We put together sure states of various sizes and watch them evolve. We observe that almost all of the photons (darker colours) stay sure collectively. |
In our processor, we begin by placing two to 5 photons on adjoining websites (i.e., initializing two to 5 adjoining qubits in “1”, and the remaining qubits in “0”), after which examine how they propagate. First, we discover that within the theoretically predicted parameter regime, they continue to be caught collectively. Next, we discover that the bigger sure states transfer extra slowly across the ring, per the truth that they’re “heavier”. This may be seen within the plot above the place the lattice websites closest to Site 12, the preliminary place of the photons, stay darker than the others with growing variety of photons (nph) within the sure state, indicating that with extra photons sure collectively there’s much less propagation across the ring.
Bound States Behave Like Single Composite Particles
To extra rigorously present that the sure states certainly behave as single particles with well-defined bodily properties, we devise a technique to measure how the vitality of the particles modifications with momentum, i.e., the energy-momentum dispersion relation.
To measure the vitality of the sure state, we use the truth that the vitality distinction between two states determines how briskly their relative part grows with time. Hence, we put together the sure state in a superposition with the state that has no photons, and measure their part distinction as a perform of time and area. Then, to transform the results of this measurement to a dispersion relation, we make the most of a Fourier remodel, which interprets place and time into momentum and vitality, respectively. We’re left with the acquainted energy-momentum relationship of excitations in a lattice.
 |
| Spectroscopy of sure states. We evaluate the part accumulation of an n-photon sure state with that of the vacuum (no photons) as a perform of lattice web site and time. A 2D Fourier remodel yields the dispersion relation of the bound-state quasiparticle. |
Breaking Integrability
The above system is “integrable,” which means that it has a enough variety of conserved portions that its dynamics are constrained to a small a part of the out there computational area. In such integrable regimes, the looks of sure states is just not that stunning. In truth, sure states in comparable methods have been predicted in 2012, then noticed in 2013. However, these sure states are fragile and their existence is often thought to derive from integrability. For extra complicated methods, there’s much less symmetry and integrability is shortly misplaced. Our preliminary concept was to probe how these sure states disappear as we break integrability to higher perceive their rigidity.
To break integrability, we modify which qubits are linked with fSim gates. We add qubits in order that at alternating websites, along with hopping to every of its two nearest-neighboring websites, a photon may also hop to a 3rd web site oriented radially outward from the ring.
While a sure state is constrained to a really small a part of part area, we anticipated that the chaotic conduct related to integrability breaking would enable the system to discover the part area extra freely. This would trigger the sure states to interrupt aside. We discover that this isn’t the case. Even when the integrability breaking is so robust that the photons are equally prone to hop to the third web site as they’re to hop to both of the 2 adjoining ring websites, the sure state stays intact, as much as the decoherence impact that makes them slowly decay (see paper for particulars).
 |
| Top: New geometry to interrupt integrability. Alternating websites are linked to a 3rd web site oriented radially outward. This will increase the complexity of the system, and permits for doubtlessly chaotic conduct. Bottom: Despite this added complexity pushing the system past integrability, we discover that the 3-photon sure state stays steady even for a comparatively massive perturbation. The likelihood of remaining sure decreases slowly attributable to decoherence (see paper). |
Conclusion
We don’t but have a satisfying rationalization for this surprising resilience. We speculate that it might be associated to a phenomenon known as prethermalization, the place incommensurate vitality scales within the system can stop a system from reaching thermal equilibrium as shortly because it in any other case would. We consider additional investigations will hopefully result in new insights into many-body quantum physics, together with the interaction of prethermalization and integrability.
Acknowledgements
We want to thank our Quantum Science Communicator Katherine McCormick for her assist scripting this weblog submit.