Experimenting with autoregressive flows in TensorFlow Probability

In the first a part of this mini-series on autoregressive circulation fashions, we checked out bijectors in TensorFlow Probability (TFP), and noticed methods to use them for sampling and density estimation. We singled out the affine bijector to show the mechanics of circulation building: We begin from a distribution that’s simple to pattern from, and that permits for easy calculation of its density. Then, we connect some variety of invertible transformations, optimizing for data-likelihood below the ultimate remodeled distribution. The effectivity of that (log)chance calculation is the place normalizing flows excel: Loglikelihood below the (unknown) goal distribution is obtained as a sum of the density below the bottom distribution of the inverse-transformed knowledge plus absolutely the log determinant of the inverse Jacobian.

Now, an affine circulation will seldom be highly effective sufficient to mannequin nonlinear, advanced transformations. In constrast, autoregressive fashions have proven substantive success in density estimation in addition to pattern era. Combined with extra concerned architectures, characteristic engineering, and intensive compute, the idea of autoregressivity has powered – and is powering – state-of-the-art architectures in areas resembling picture, speech and video modeling.

This submit will likely be involved with the constructing blocks of autoregressive flows in TFP. While we gained’t precisely be constructing state-of-the-art fashions, we’ll attempt to perceive and play with some main elements, hopefully enabling the reader to do her personal experiments on her personal knowledge.

This submit has three components: First, we’ll take a look at autoregressivity and its implementation in TFP. Then, we attempt to (roughly) reproduce one of many experiments within the “MAF paper” (Masked Autoregressive Flows for Distribution Estimation (Papamakarios, Pavlakou, and Murray 2017)) – primarily a proof of idea. Finally, for the third time on this weblog, we come again to the duty of analysing audio knowledge, with blended outcomes.

Autoregressivity and masking

In distribution estimation, autoregressivity enters the scene through the chain rule of likelihood that decomposes a joint density right into a product of conditional densities:

[
p(mathbf{x}) = prod_{i}p(mathbf{x}_i|mathbf{x}_{1:i−1})
]

In apply, because of this autoregressive fashions must impose an order on the variables – an order which could or won’t “make sense.” Approaches right here embody selecting orderings at random and/or utilizing totally different orderings for every layer.
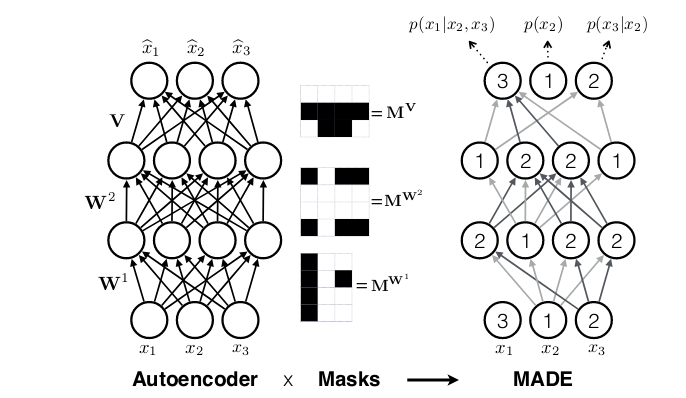
While in recurrent neural networks, autoregressivity is conserved because of the recurrence relation inherent in state updating, it isn’t clear a priori how autoregressivity is to be achieved in a densely related structure. A computationally environment friendly answer was proposed in MADE: Masked Autoencoder for Distribution Estimation(Germain et al. 2015): Starting from a densely related layer, masks out all connections that shouldn’t be allowed, i.e., all connections from enter characteristic (i) to stated layer’s activations (1 … i-1). Or expressed in another way, activation (i) could also be related to enter options (1 … i-1) solely. Then when including extra layers, care should be taken to make sure that all required connections are masked in order that on the finish, output (i) will solely ever have seen inputs (1 … i-1).

Thus masked autoregressive flows are a fusion of two main approaches – autoregressive fashions (which needn’t be flows) and flows (which needn’t be autoregressive). In TFP these are offered by MaskedAutoregressiveFlow, for use as a bijector in a TransformedDistribution.

While the documentation exhibits methods to use this bijector, the step from theoretical understanding to coding a “black box” could seem broad. If you’re something just like the creator, right here you may really feel the urge to “look under the hood” and confirm that issues actually are the way in which you’re assuming. So let’s give in to curiosity and permit ourselves a little bit escapade into the supply code.

Peeking forward, that is how we’ll assemble a masked autoregressive circulation in TFP (once more utilizing the nonetheless new-ish R bindings offered by tfprobability):

library(tfprobability)

maf <- tfb_masked_autoregressive_flow(
    shift_and_log_scale_fn = tfb_masked_autoregressive_default_template(
      hidden_layers = record(num_hidden, num_hidden),
      activation = tf$nn$tanh)
)

Pulling aside the related entities right here, tfb_masked_autoregressive_flow is a bijector, with the standard strategies tfb_forward(), tfb_inverse(), tfb_forward_log_det_jacobian() and tfb_inverse_log_det_jacobian().
The default shift_and_log_scale_fn, tfb_masked_autoregressive_default_template, constructs a little bit neural community of its personal, with a configurable variety of hidden models per layer, a configurable activation perform and optionally, different configurable parameters to be handed to the underlying dense layers. It’s these dense layers that must respect the autoregressive property. Can we check out how that is performed? Yes we will, offered we’re not afraid of a little bit Python.

masked_autoregressive_default_template (now leaving out the tfb_ as we’ve entered Python-land) makes use of masked_dense to do what you’d suppose a thus-named perform is likely to be doing: assemble a dense layer that has a part of the load matrix masked out. How? We’ll see after a number of Python setup statements.

import numpy as np
import tensorflow as tf
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
tf.enable_eager_execution()

The following code snippets are taken from masked_dense (in its present kind on grasp), and when attainable, simplified for higher readability, accommodating simply the specifics of the chosen instance – a toy matrix of form 2×3:

# assemble some toy enter knowledge (this line clearly not from the unique code)
inputs = tf.fixed(np.arange(1.,7), form = (2, 3))

# (partly) decide form of masks from form of enter
input_depth = tf.compat.dimension_value(inputs.form.with_rank_at_least(1)[-1])
num_blocks = input_depth
num_blocks # 3

Our toy layer ought to have 4 models:

The masks is initialized to all zeros. Considering it is going to be used to elementwise multiply the load matrix, we’re a bit stunned at its form (shouldn’t it’s the opposite approach spherical?). No worries; all will prove appropriate ultimately.

masks = np.zeros([units, input_depth], dtype=tf.float32.as_numpy_dtype())
masks

array([[0., 0., 0.],
       [0., 0., 0.],
       [0., 0., 0.],
       [0., 0., 0.]], dtype=float32)

Now to “whitelist” the allowed connections, we’ve to fill in ones each time data circulation is allowed by the autoregressive property:

def _gen_slices(num_blocks, n_in, n_out):
  slices = []
  col = 0
  d_in = n_in // num_blocks
  d_out = n_out // num_blocks
  row = d_out 
  for _ in vary(num_blocks):
    row_slice = slice(row, None)
    col_slice = slice(col, col + d_in)
    slices.append([row_slice, col_slice])
    col += d_in
    row += d_out
  return slices

slices = _gen_slices(num_blocks, input_depth, models)
for [row_slice, col_slice] in slices:
  masks[row_slice, col_slice] = 1

masks

array([[0., 0., 0.],
       [1., 0., 0.],
       [1., 1., 0.],
       [1., 1., 1.]], dtype=float32)

Again, does this look mirror-inverted? A transpose fixes form and logic each:

array([[0., 1., 1., 1.],
       [0., 0., 1., 1.],
       [0., 0., 0., 1.]], dtype=float32)

Now that we’ve the masks, we will create the layer (curiously, as of this writing not (but?) a tf.keras layer):

layer = tf.compat.v1.layers.Dense(
        models,
        kernel_initializer=masked_initializer, # 1
        kernel_constraint=lambda x: masks * x   # 2
        )

Here we see masking occurring in two methods. For one, the load initializer is masked:

kernel_initializer = tf.compat.v1.glorot_normal_initializer()

def masked_initializer(form, dtype=None, partition_info=None):
 return masks * kernel_initializer(form, dtype, partition_info)

And secondly, a kernel constraint makes certain that after optimization, the relative models are zeroed out once more:

kernel_constraint=lambda x: masks * x 

Just for enjoyable, let’s apply the layer to our toy enter:

<tf.Tensor: id=30, form=(2, 4), dtype=float64, numpy=
array([[ 0.        , -0.7489589 , -0.43329933,  1.42710014],
       [ 0.        , -2.9958356 , -1.71647246,  1.09258015]])>

Zeroes the place anticipated. And double-checking on the load matrix…

<tf.Variable 'dense/kernel:0' form=(3, 4) dtype=float64, numpy=
array([[ 0.        , -0.7489589 , -0.42214942, -0.6473454 ],
       [-0.        ,  0.        , -0.00557496, -0.46692933],
       [-0.        , -0.        , -0.        ,  1.00276807]])>

Good. Now hopefully after this little deep dive, issues have turn into a bit extra concrete. Of course in an even bigger mannequin, the autoregressive property needs to be conserved between layers as nicely.

On to the second matter, utility of MAF to a real-world dataset.

Masked Autoregressive Flow

The MAF paper(Papamakarios, Pavlakou, and Murray 2017) utilized masked autoregressive flows (in addition to single-layer-MADE(Germain et al. 2015) and Real NVP (Dinh, Sohl-Dickstein, and Bengio 2016)) to numerous datasets, together with MNIST, CIFAR-10 and a number of other datasets from the UCI Machine Learning Repository.

We decide one of many UCI datasets: Gas sensors for dwelling exercise monitoring. On this dataset, the MAF authors obtained the very best outcomes utilizing a MAF with 10 flows, so that is what we are going to attempt.

Collecting data from the paper, we all know that

• knowledge was included from the file ethylene_CO.txt solely;
• discrete columns have been eradicated, in addition to all columns with correlations > .98; and
• the remaining 8 columns have been standardised (z-transformed).

Regarding the neural community structure, we collect that

• every of the ten MAF layers was adopted by a batchnorm;
• as to characteristic order, the primary MAF layer used the variable order that got here with the dataset; then each consecutive layer reversed it;
• particularly for this dataset and versus all different UCI datasets, tanh was used for activation as a substitute of relu;
• the Adam optimizer was used, with a studying fee of 1e-4;
• there have been two hidden layers for every MAF, with 100 models every;
• coaching went on till no enchancment occurred for 30 consecutive epochs on the validation set; and
• the bottom distribution was a multivariate Gaussian.

This is all helpful data for our try and estimate this dataset, however the important bit is that this. In case you knew the dataset already, you might need been questioning how the authors would cope with the dimensionality of the info: It is a time collection, and the MADE structure explored above introduces autoregressivity between options, not time steps. So how is the extra temporal autoregressivity to be dealt with? The reply is: The time dimension is actually eliminated. In the authors’ phrases,

[…] it’s a time collection however was handled as if every instance have been an i.i.d. pattern from the marginal distribution.

This undoubtedly is beneficial data for our current modeling try, nevertheless it additionally tells us one thing else: We might need to look past MADE layers for precise time collection modeling.

Now although let’s take a look at this instance of utilizing MAF for multivariate modeling, with no time or spatial dimension to be taken into consideration.

Following the hints the authors gave us, that is what we do.

Observations: 4,208,261
Variables: 19
$ X1  <dbl> 0.00, 0.01, 0.01, 0.03, 0.04, 0.05, 0.06, 0.07, 0.07, 0.09,...
$ X2  <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,...
$ X3  <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,...
$ X4  <dbl> -50.85, -49.40, -40.04, -47.14, -33.58, -48.59, -48.27, -47.14,... 
$ X5  <dbl> -1.95, -5.53, -16.09, -10.57, -20.79, -11.54, -9.11, -4.56,...
$ X6  <dbl> -41.82, -42.78, -27.59, -32.28, -33.25, -36.16, -31.31, -16.57,... 
$ X7  <dbl> 1.30, 0.49, 0.00, 4.40, 6.03, 6.03, 5.37, 4.40, 23.98, 2.77,...
$ X8  <dbl> -4.07, 3.58, -7.16, -11.22, 3.42, 0.33, -7.97, -2.28, -2.12,...
$ X9  <dbl> -28.73, -34.55, -42.14, -37.94, -34.22, -29.05, -30.34, -24.35,...
$ X10 <dbl> -13.49, -9.59, -12.52, -7.16, -14.46, -16.74, -8.62, -13.17,...
$ X11 <dbl> -3.25, 5.37, -5.86, -1.14, 8.31, -1.14, 7.00, -6.34, -0.81,...
$ X12 <dbl> 55139.95, 54395.77, 53960.02, 53047.71, 52700.28, 51910.52,...
$ X13 <dbl> 50669.50, 50046.91, 49299.30, 48907.00, 48330.96, 47609.00,...
$ X14 <dbl> 9626.26, 9433.20, 9324.40, 9170.64, 9073.64, 8982.88, 8860.51,...
$ X15 <dbl> 9762.62, 9591.21, 9449.81, 9305.58, 9163.47, 9021.08, 8966.48,...
$ X16 <dbl> 24544.02, 24137.13, 23628.90, 23101.66, 22689.54, 22159.12,...
$ X17 <dbl> 21420.68, 20930.33, 20504.94, 20101.42, 19694.07, 19332.57,...
$ X18 <dbl> 7650.61, 7498.79, 7369.67, 7285.13, 7156.74, 7067.61, 6976.13,...
$ X19 <dbl> 6928.42, 6800.66, 6697.47, 6578.52, 6468.32, 6385.31, 6300.97,...

# we do not know if we'll find yourself with the identical columns because the authors did,
# however we attempt (a minimum of we do find yourself with 8 columns)
df <- df[,-(1:3)]
hc <- findCorrelation(cor(df), cutoff = 0.985)
df2 <- df[,-c(hc)]

# scale
df2 <- scale(df2)
df2

# A tibble: 4,208,261 x 8
      X4     X5     X8    X9    X13    X16    X17   X18
   <dbl>  <dbl>  <dbl> <dbl>  <dbl>  <dbl>  <dbl> <dbl>
 1 -50.8  -1.95  -4.07 -28.7 50670. 24544. 21421. 7651.
 2 -49.4  -5.53   3.58 -34.6 50047. 24137. 20930. 7499.
 3 -40.0 -16.1   -7.16 -42.1 49299. 23629. 20505. 7370.
 4 -47.1 -10.6  -11.2  -37.9 48907  23102. 20101. 7285.
 5 -33.6 -20.8    3.42 -34.2 48331. 22690. 19694. 7157.
 6 -48.6 -11.5    0.33 -29.0 47609  22159. 19333. 7068.
 7 -48.3  -9.11  -7.97 -30.3 47047. 21932. 19028. 6976.
 8 -47.1  -4.56  -2.28 -24.4 46758. 21504. 18780. 6900.
 9 -42.3  -2.77  -2.12 -27.6 46197. 21125. 18439. 6827.
10 -44.6   3.58  -0.65 -35.5 45652. 20836. 18209. 6790.
# … with 4,208,251 extra rows

Now arrange the info era course of:

# train-test cut up
n_rows <- nrow(df2) # 4208261
train_ids <- pattern(1:n_rows, 0.5 * n_rows)
x_train <- df2[train_ids, ]
x_test <- df2[-train_ids, ]

# create datasets
batch_size <- 100
train_dataset <- tf$solid(x_train, tf$float32) %>%
  tensor_slices_dataset %>%
  dataset_batch(batch_size)

test_dataset <- tf$solid(x_test, tf$float32) %>%
  tensor_slices_dataset %>%
  dataset_batch(nrow(x_test))

To assemble the circulation, the very first thing wanted is the bottom distribution.

base_dist <- tfd_multivariate_normal_diag(loc = rep(0, ncol(df2)))

Now for the circulation, by default constructed with batchnorm and permutation of characteristic order.

num_hidden <- 100
dim <- ncol(df2)

use_batchnorm <- TRUE
use_permute <- TRUE
num_mafs <-10
num_layers <- 3 * num_mafs

bijectors <- vector(mode = "record", size = num_layers)

for (i in seq(1, num_layers, by = 3)) {
  maf <- tfb_masked_autoregressive_flow(
    shift_and_log_scale_fn = tfb_masked_autoregressive_default_template(
      hidden_layers = record(num_hidden, num_hidden),
      activation = tf$nn$tanh))
  bijectors[[i]] <- maf
  if (use_batchnorm)
    bijectors[[i + 1]] <- tfb_batch_normalization()
  if (use_permute)
    bijectors[[i + 2]] <- tfb_permute((ncol(df2) - 1):0)
}

if (use_permute) bijectors <- bijectors[-num_layers]

circulation <- bijectors %>%
  discard(is.null) %>%
  # tfb_chain expects arguments in reverse order of utility
  rev() %>%
  tfb_chain()

target_dist <- tfd_transformed_distribution(
  distribution = base_dist,
  bijector = circulation
)

And configuring the optimizer:

optimizer <- tf$prepare$AdamOptimizer(1e-4)

Under that isotropic Gaussian we selected as a base distribution, how doubtless are the info?

base_loglik <- base_dist %>% 
  tfd_log_prob(x_train) %>% 
  tf$reduce_mean()
base_loglik %>% as.numeric()        # -11.33871

base_loglik_test <- base_dist %>% 
  tfd_log_prob(x_test) %>% 
  tf$reduce_mean()
base_loglik_test %>% as.numeric()   # -11.36431

And, simply as a fast sanity examine: What is the loglikelihood of the info below the remodeled distribution earlier than any coaching?

target_loglik_pre <-
  target_dist %>% tfd_log_prob(x_train) %>% tf$reduce_mean()
target_loglik_pre %>% as.numeric()        # -11.22097

target_loglik_pre_test <-
  target_dist %>% tfd_log_prob(x_test) %>% tf$reduce_mean()
target_loglik_pre_test %>% as.numeric()   # -11.36431

The values match – good. Here now could be the coaching loop. Being impatient, we already hold checking the loglikelihood on the (full) check set to see if we’re making any progress.

n_epochs <- 10

for (i in 1:n_epochs) {
  
  agg_loglik <- 0
  num_batches <- 0
  iter <- make_iterator_one_shot(train_dataset)
  
  until_out_of_range({
    batch <- iterator_get_next(iter)
    loss <-
      perform()
        - tf$reduce_mean(target_dist %>% tfd_log_prob(batch))
    optimizer$decrease(loss)
    
    loglik <- tf$reduce_mean(target_dist %>% tfd_log_prob(batch))
    agg_loglik <- agg_loglik + loglik
    num_batches <- num_batches + 1
    
    test_iter <- make_iterator_one_shot(test_dataset)
    test_batch <- iterator_get_next(test_iter)
    loglik_test_current <- target_dist %>% tfd_log_prob(test_batch) %>% tf$reduce_mean()
    
    if (num_batches %% 100 == 1)
      cat(
        "Epoch ",
        i,
        ": ",
        "Batch ",
        num_batches,
        ": ",
        (agg_loglik %>% as.numeric()) / num_batches,
        " --- check: ",
        loglik_test_current %>% as.numeric(),
        "n"
      )
  })
}

With each coaching and check units amounting to over 2 million information every, we didn’t have the endurance to run this mannequin till no enchancment occurred for 30 consecutive epochs on the validation set (just like the authors did). However, the image we get from one full epoch’s run is fairly clear: The setup appears to work fairly okay.

Epoch  1 :  Batch      1:  -8.212026  --- check:  -10.09264 
Epoch  1 :  Batch   1001:   2.222953  --- check:   1.894102 
Epoch  1 :  Batch   2001:   2.810996  --- check:   2.147804 
Epoch  1 :  Batch   3001:   3.136733  --- check:   3.673271 
Epoch  1 :  Batch   4001:   3.335549  --- check:   4.298822 
Epoch  1 :  Batch   5001:   3.474280  --- check:   4.502975 
Epoch  1 :  Batch   6001:   3.606634  --- check:   4.612468 
Epoch  1 :  Batch   7001:   3.695355  --- check:   4.146113 
Epoch  1 :  Batch   8001:   3.767195  --- check:   3.770533 
Epoch  1 :  Batch   9001:   3.837641  --- check:   4.819314 
Epoch  1 :  Batch  10001:   3.908756  --- check:   4.909763 
Epoch  1 :  Batch  11001:   3.972645  --- check:   3.234356 
Epoch  1 :  Batch  12001:   4.020613  --- check:   5.064850 
Epoch  1 :  Batch  13001:   4.067531  --- check:   4.916662 
Epoch  1 :  Batch  14001:   4.108388  --- check:   4.857317 
Epoch  1 :  Batch  15001:   4.147848  --- check:   5.146242 
Epoch  1 :  Batch  16001:   4.177426  --- check:   4.929565 
Epoch  1 :  Batch  17001:   4.209732  --- check:   4.840716 
Epoch  1 :  Batch  18001:   4.239204  --- check:   5.222693 
Epoch  1 :  Batch  19001:   4.264639  --- check:   5.279918 
Epoch  1 :  Batch  20001:   4.291542  --- check:   5.29119 
Epoch  1 :  Batch  21001:   4.314462  --- check:   4.872157 
Epoch  2 :  Batch      1:   5.212013  --- check:   4.969406 

With these coaching outcomes, we regard the proof of idea as mainly profitable. However, from our experiments we additionally must say that the selection of hyperparameters appears to matter a lot. For instance, use of the relu activation perform as a substitute of tanh resulted within the community mainly studying nothing. (As per the authors, relu labored wonderful on different datasets that had been z-transformed in simply the identical approach.)

Batch normalization right here was compulsory – and this may go for flows typically. The permutation bijectors, then again, didn’t make a lot of a distinction on this dataset. Overall the impression is that for flows, we would both want a “bag of tricks” (like is often stated about GANs), or extra concerned architectures (see “Outlook” under).

Finally, we wind up with an experiment, coming again to our favourite audio knowledge, already featured in two posts: Simple Audio Classification with Keras and Audio classification with Keras: Looking nearer on the non-deep studying components.

Analysing audio knowledge with MAF

The dataset in query consists of recordings of 30 phrases, pronounced by numerous totally different audio system. In these earlier posts, a convnet was educated to map spectrograms to these 30 courses. Now as a substitute we wish to attempt one thing totally different: Train an MAF on one of many courses – the phrase “zero,” say – and see if we will use the educated community to mark “non-zero” phrases as much less doubtless: carry out anomaly detection, in a approach. Spoiler alert: The outcomes weren’t too encouraging, and if you’re fascinated by a activity like this, you may wish to contemplate a distinct structure (once more, see “Outlook” under).

Nonetheless, we rapidly relate what was performed, as this activity is a pleasant instance of dealing with knowledge the place options differ over multiple axis.

Preprocessing begins as within the aforementioned earlier posts. Here although, we explicitly use keen execution, and should generally hard-code recognized values to maintain the code snippets brief.

library(tensorflow)
library(tfprobability)

tfe_enable_eager_execution(device_policy = "silent")

library(tfdatasets)
library(dplyr)
library(readr)
library(purrr)
library(caret)
library(stringr)

# make decode_wav() run with the present launch 1.13.1 in addition to with the present grasp department
decode_wav <- perform() if (reticulate::py_has_attr(tf, "audio")) tf$audio$decode_wav
  else tf$contrib$framework$python$ops$audio_ops$decode_wav
# similar for stft()
stft <- perform() if (reticulate::py_has_attr(tf, "sign")) tf$sign$stft else tf$spectral$stft

information <- fs::dir_ls(path = "audio/data_1/speech_commands_v0.01/", # change by yours
                    recursive = TRUE,
                    glob = "*.wav")

information <- information[!str_detect(files, "background_noise")]

df <- tibble(
  fname = information,
  class = fname %>%
    str_extract("v0.01/.*/") %>%
    str_replace_all("v0.01/", "") %>%
    str_replace_all("/", "")
)

We prepare the MAF on pronunciations of the phrase “zero.”

Following the method detailed in Audio classification with Keras: Looking nearer on the non-deep studying components, we’d like to coach the community on spectrograms as a substitute of the uncooked time area knowledge.
Using the identical settings for frame_length and frame_step of the Short Term Fourier Transform as in that submit, we’d arrive at knowledge formed variety of frames x variety of FFT coefficients. To make this work with the masked_dense() employed in tfb_masked_autoregressive_flow(), the info would then must be flattened, yielding a powerful 25186 options within the joint distribution.

With the structure outlined as above within the GAS instance, this result in the community not making a lot progress. Neither did leaving the info in time area kind, with 16000 options within the joint distribution. Thus, we determined to work with the FFT coefficients computed over the entire window as a substitute, leading to 257 joint options.

batch_size <- 100

sampling_rate <- 16000L
data_generator <- perform(df,
                           batch_size) {
  
  ds <- tensor_slices_dataset(df) 
  
  ds <- ds %>%
    dataset_map(perform(obs) {
      wav <-
        decode_wav()(tf$read_file(tf$reshape(obs$fname, record())))
      samples <- wav$audio[ ,1]
      
      # some wave information have fewer than 16000 samples
      padding <- record(record(0L, sampling_rate - tf$form(samples)[1]))
      padded <- tf$pad(samples, padding)
      
      stft_out <- stft()(padded, 16000L, 1L, 512L)
      magnitude_spectrograms <- tf$abs(stft_out) %>% tf$squeeze()
    })
  
  ds %>% dataset_batch(batch_size)
  
}

ds_train <- data_generator(df_train, batch_size)
batch <- ds_train %>% 
  make_iterator_one_shot() %>%
  iterator_get_next()

dim(batch) # 100 x 257

Training then proceeded as on the GAS dataset.

# outline MAF
base_dist <-
  tfd_multivariate_normal_diag(loc = rep(0, dim(batch)[2]))

num_hidden <- 512 
use_batchnorm <- TRUE
use_permute <- TRUE
num_mafs <- 10 
num_layers <- 3 * num_mafs

# retailer bijectors in an inventory
bijectors <- vector(mode = "record", size = num_layers)

# fill record, optionally including batchnorm and permute bijectors
for (i in seq(1, num_layers, by = 3)) {
  maf <- tfb_masked_autoregressive_flow(
    shift_and_log_scale_fn = tfb_masked_autoregressive_default_template(
      hidden_layers = record(num_hidden, num_hidden),
      activation = tf$nn$tanh,
      ))
  bijectors[[i]] <- maf
  if (use_batchnorm)
    bijectors[[i + 1]] <- tfb_batch_normalization()
  if (use_permute)
    bijectors[[i + 2]] <- tfb_permute((dim(batch)[2] - 1):0)
}

if (use_permute) bijectors <- bijectors[-num_layers]
circulation <- bijectors %>%
  # probably clear out empty components (if no batchnorm or no permute)
  discard(is.null) %>%
  rev() %>%
  tfb_chain()

target_dist <- tfd_transformed_distribution(distribution = base_dist,
                                            bijector = circulation)

optimizer <- tf$prepare$AdamOptimizer(1e-3)

# prepare MAF
n_epochs <- 100
for (i in 1:n_epochs) {
  agg_loglik <- 0
  num_batches <- 0
  iter <- make_iterator_one_shot(ds_train)
  until_out_of_range({
    batch <- iterator_get_next(iter)
    loss <-
      perform()
        - tf$reduce_mean(target_dist %>% tfd_log_prob(batch))
    optimizer$decrease(loss)
    
    loglik <- tf$reduce_mean(target_dist %>% tfd_log_prob(batch))
    agg_loglik <- agg_loglik + loglik
    num_batches <- num_batches + 1
    
    loglik_test_current <- 
      target_dist %>% tfd_log_prob(ds_test) %>% tf$reduce_mean()

    if (num_batches %% 20 == 1)
      cat(
        "Epoch ",
        i,
        ": ",
        "Batch ",
        num_batches,
        ": ",
        ((agg_loglik %>% as.numeric()) / num_batches) %>% spherical(1),
        " --- check: ",
        loglik_test_current %>% as.numeric() %>% spherical(1),
        "n"
      )
  })
}

During coaching, we additionally monitored loglikelihoods on three totally different courses, cat, hen and wow. Here are the loglikelihoods from the primary 10 epochs. “Batch” refers back to the present coaching batch (first batch within the epoch), all different values refer to finish datasets (the entire check set and the three units chosen for comparability).

epoch   |   batch  |   check   |   "cat"  |   "hen"  |   "wow"  |
--------|----------|----------|----------|-----------|----------|
1       |   1443.5 |   1455.2 |   1398.8 |    1434.2 |   1546.0 |
2       |   1935.0 |   2027.0 |   1941.2 |    1952.3 |   2008.1 | 
3       |   2004.9 |   2073.1 |   2003.5 |    2000.2 |   2072.1 |
4       |   2063.5 |   2131.7 |   2056.0 |    2061.0 |   2116.4 |        
5       |   2120.5 |   2172.6 |   2096.2 |    2085.6 |   2150.1 |
6       |   2151.3 |   2206.4 |   2127.5 |    2110.2 |   2180.6 | 
7       |   2174.4 |   2224.8 |   2142.9 |    2163.2 |   2195.8 |
8       |   2203.2 |   2250.8 |   2172.0 |    2061.0 |   2221.8 |        
9       |   2224.6 |   2270.2 |   2186.6 |    2193.7 |   2241.8 |
10      |   2236.4 |   2274.3 |   2191.4 |    2199.7 |   2243.8 |        

While this doesn’t look too unhealthy, a whole comparability towards all twenty-nine non-target courses had “zero” outperformed by seven different courses, with the remaining twenty-two decrease in loglikelihood. We don’t have a mannequin for anomaly detection, as but.

Outlook

As already alluded to a number of occasions, for knowledge with temporal and/or spatial orderings extra advanced architectures might show helpful. The very profitable PixelCNN household relies on masked convolutions, with newer developments bringing additional refinements (e.g. Gated PixelCNN (Oord et al. 2016), PixelCNN++ (Salimans et al. 2017). Attention, too, could also be masked and thus rendered autoregressive, as employed within the hybrid PixelSNAIL (Chen et al. 2017) and the – not surprisingly given its title – transformer-based ImageTransformer (Parmar et al. 2018).

To conclude, – whereas this submit was within the intersection of flows and autoregressivity – and final not least the use therein of TFP bijectors – an upcoming one may dive deeper into autoregressive fashions particularly… and who is aware of, maybe come again to the audio knowledge for a fourth time.